
【题目】已知,如图,在△ABC中,AE平分∠CAB交BC于点E,AC=6,CE=3,![]() ,BE=5,点F是边AB上的动点(点F与点A,B不重合),联结EF,设BF=x,EF=y.
,BE=5,点F是边AB上的动点(点F与点A,B不重合),联结EF,设BF=x,EF=y.
(1)求AB的长;
(2)求y关于x的函数解析式,并写出函数的定义域;
(3)当△AEF为等腰三角形时,直接写出BF的长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气严重影响市民的生活质量。在今年寒假期间,某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了下图所示的不完整的统计图表:
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 |
|
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) |
|
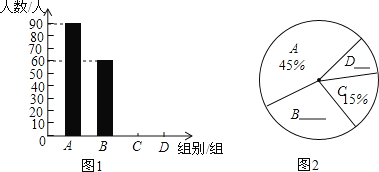
请根据统计图表回答下列问题:
(1)本次被调查的市民共有多少人?并求![]() 和
和![]() 的值;
的值;
(2)请补全条形统计图,并计算扇形统计图中扇形区域![]() 所对应的圆心角的度数;
所对应的圆心角的度数;
(3)若该市有100万人口,请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
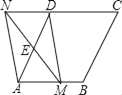
【题目】如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为 时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时18分钟,他骑自行车的平均速度是300米/分钟,步行的平均速度是120米/分钟,他家离学校的距离是4500米.
(1)李明上学时骑自行车的路程和步行的路程分别为多少米?
(2)放学后李明从17:40开始离校回家,但此时道路施工的地段增长了600米,如果按照上学时的速度,问李明能否在18:00之前到家?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com