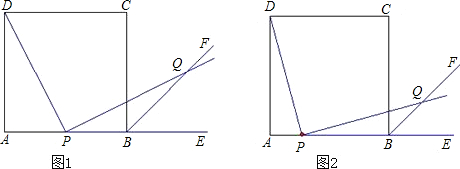
边长为1的正方形ABCD中,E,F为对角线BD上的动点.
(Ⅰ)证明:AE+AF=CE+CF;
(Ⅱ)①求AE+CE的最小值;②求AE+BE+CE的最小值;
(Ⅲ)若∠EAF=45°,DF=2BE,求四边形AECF的面积.
(I)证明:

∵AB=BC,∠ABE=∠CBE,BE=BE,
∴△ABE≌△CBE,
∴AE=CE,
同理:AF=CF.
∴AE+AF=CE+CF.
(Ⅱ)解:①当A,C,E在同一直线上是最短的.
∴AC=AE+EC=

.
②当B点和E点重合时是最短的.
AE+BE+CE=AB+BC=2.
(Ⅲ)解:连接AC交BD于O,设DF=2x,BE=x,

由勾股定理得:AO=

=BO=OD,BD=

,
即EF=BD-BE-DF=

-3x,DE=BD-BE=

-x,
∵四边形ABCD是正方形,
∴∠ADB=45°=∠EAF,
∵∠AEF=∠AEF,
∴△AEF∽△DEA,
∴
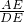
=

,
∴AE
2=DE•EF=(

-x)•(

-3x),
在直角三角形AEO中,由勾股定理得:AE
2=AO
2+EO
2=

+

,
∴(

-x)(

-3x)=

+

,
解得:x=

>

(舍去),x=

,
∴EF=

-3x=

∴四边形AECF的面积是

EF×AC=

×

×

=

.
分析:(I)根据全等三角形判定和正方形性质求出△ABE≌△CBE,推出AF=CF,AE=CE即可;
(II)根据两点之间线段最短,求出点E的位置即可;
(III)连接AC交BD于O,设DF=2x,BE=x,由正方形性质和勾股定理求出AO,OB,AC,BD的长,证△AEF∽△DEA,求出AE的平方的值,在Rt△AOE中,根据勾股定理求出AE的平方的值,得出方程,求出x的值,根据面积公式求出即可.
点评:本题综合运用了正方形的性质,全等三角形的性质和判定,勾股定理,轴对称和最短问题等知识点,此题有一点难度,对学生有较高的要求,第三问得出关于x的方程是解此题的难点.

 ∵AB=BC,∠ABE=∠CBE,BE=BE,
∵AB=BC,∠ABE=∠CBE,BE=BE, .
. 由勾股定理得:AO=
由勾股定理得:AO= =BO=OD,BD=
=BO=OD,BD= ,
, -3x,DE=BD-BE=
-3x,DE=BD-BE= -x,
-x,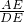 =
= ,
, -x)•(
-x)•( -3x),
-3x), +
+ ,
, -x)(
-x)( -3x)=
-3x)= +
+ ,
, >
> (舍去),x=
(舍去),x= ,
, -3x=
-3x=
 EF×AC=
EF×AC= ×
× ×
× =
= .
.