
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果 ,求
,求 的值.
的值.

他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为???? ,CG和EH的数量关系为???? , 的值为???? .
的值为???? .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为???? (用含a的代数式表示).
的值为???? (用含a的代数式表示).

(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为???? (用含m,n的代数式表示).
的值为???? (用含m,n的代数式表示).

(1)3,2, ;(2)
;(2) ;(3)mn.
;(3)mn.
【解析】
试题分析:(1)过E点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH来表示,最后求得比值;
(2)先作EH∥AB交BG于点H,得出△EFH∽△AFB,即可得出 ,再根据AB=CD,表示出CD,根据平行线的性质得出△BEH∽△BCG,即可表示出
,再根据AB=CD,表示出CD,根据平行线的性质得出△BEH∽△BCG,即可表示出 ,从而得出
,从而得出 的值;
的值;
(3)先过点E作EH∥AB交BD的延长线于点H,得出EH∥AB∥CD,根据EH∥CD,得出△BCD∽△BEH,再进一步证出△ABF∽△EHF,从而得出 的值.
的值.
试题解析:(1)过点E作EH∥AB交BG于点H,
则有△ABF∽△HEF,
∴ ,
,
∴AB=3EH.
∵平行四边形ABCD中,EH∥AB,
∴EH∥CD,
又∵E为BC中点,
∴EH为△BCG的中位线,
∴CG=2EH,
∴ ;
;
(2)作EH∥AB交BG于点H,则△EFH∽△AFB,
∴ ,
,
∴AB=aEH.
∵AB=CD,
∴CD=aEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴ ,
,
∴CG=2EH.
∴ ;
;
(3)过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD,
∵EH∥CD,
∴△BCD∽△BEH,
∴ ,
,
∴CD=nEH.
又 ,
,
∴AB=mCD=mnEH.
∵EH∥AB,
∴△ABF∽△EHF,
∴ .
.
考点:相似形综合题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:阅读理解
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2013届北京市西城区(北区)九年级上学期期末考试数学试卷(带解析) 题型:解答题
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对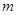 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则 时,
时, 的最大值为
的最大值为 .
.
请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京海淀区九年级第一学期期中测评数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明在研究中心对称问题时发现:
如图1,当点 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 旋转180°得到
旋转180°得到 点,这时点
点,这时点 与点
与点 重合.
重合.
如图2,当点 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.



(1)请在图2中画出点 、
、 ,
小明在证明P、
,
小明在证明P、 两点关于点
两点关于点 中心对称时,除了说明P、
中心对称时,除了说明P、 、
、 三点共线之外,还需证明;
三点共线之外,还需证明;
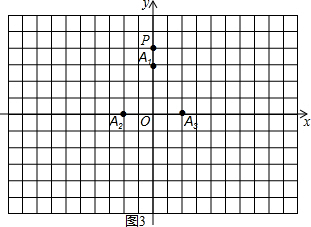
(2)如图3,在平面直角坐标系xOy中,当 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐标为(),点
的坐标为(),点 的坐为.
的坐为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com