
【题目】如图△ABC中,∠C=90°,∠A=30°,B C=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
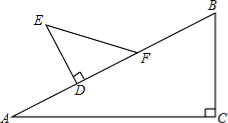
(1) 当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行.
(2) 在△DEF的移动过程中,是否存在某个位置,使得∠EBD=22.5°?如果存在,求出AD的长度;如果不存在,请说明理由.
【答案】(1) ![]() cm;(2)
cm;(2)![]() cm.
cm.
【解析】
试题(1)因为∠C=90°,∠A=30°,BC=5cm,所以AB=10cm,又因为∠FDE=90°,∠DEF=45°,DE=3cm,所以DE=4cm,连接EB,设BE∥AC,则可求证∠EBD=∠A=30°,故AD的长度可求;
(2)当∠EBD=22.5°时,利用三角形外角的性质求得∠BEF=22.5°,则∠EBD=∠BEF,故BF=EF=![]() ,AD=BD-BF-DF=
,AD=BD-BF-DF=![]() (cm);
(cm);
试题解析:(1)![]() cm时,BE∥AC.理由如下:
cm时,BE∥AC.理由如下:
设EB∥AC,则∠EBD=∠A=30°,
∴在Rt△EBD中,![]() cm
cm
∴![]() cm
cm
∴![]() cm时,BE∥AC;
cm时,BE∥AC;
(2) 在△DEF的移动过程中,当AD=![]() cm时,使得∠EBD=22.5°.理由如下:
cm时,使得∠EBD=22.5°.理由如下:
假设∠EBD=22.5°.
∵在△DEF中,∠D=90°,∠DEF=45°,DE=3cm,
∴EF=![]() cm,∠DEF=∠DFE=45°,DE=DF=3cm.
cm,∠DEF=∠DFE=45°,DE=DF=3cm.
又∵∠DFE=∠FEB+∠FBE=45°,
∴∠EBD=∠BEF,
∴BF=EF=![]() ,
,
∴AD=BD-BF-DF=![]() (cm).
(cm).
∴在△DEF的移动过程中,当AD=![]() cm时,使得∠EBD=22.5°.
cm时,使得∠EBD=22.5°.
考点: 几何变换综合题


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
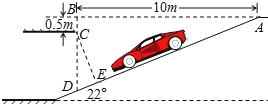
【题目】如图是菏泽银座地下停车场入口的设计图,请根据图中数据计算 CE的长度.(结果精确到 0.01m,参考数据:sin22°≈0.3746,cos22°≈0.9272, tan22°≈0.4040)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得到△EDC,当点B的对应点D恰好落在AC边上时,∠CAE的度数为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
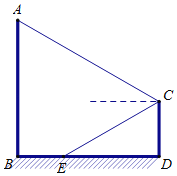
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
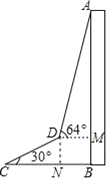
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的![]() ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为1,顶点B与原点O重合,点C在x轴的正半轴上,过点B作BA1⊥AC于点A1,过点A1作A1B1∥OA,交OC于点B1;过点B1作B1A2⊥AC于点A2,过点A2作A2B2∥OA,交OC于点B2;……,按此规律进行下去,点A2020的坐标是_____________.
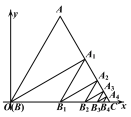
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接BE.DE=12,
(1)若CD=4,求⊙O的半径;
(2)若AD+CD=30,求AC的长.
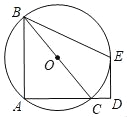
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,以
上一点,以![]() 为圆心,OA为半径的圆分别交AB,AC于点E,D,在
为圆心,OA为半径的圆分别交AB,AC于点E,D,在![]() 的延长线上取点
的延长线上取点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)OA=4, ∠A=30°,求图中线段DG、线段EG与弧DE围成阴影部分的面积.
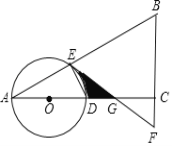
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com