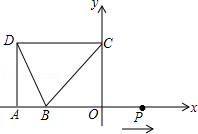
解:(1)∵D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,
∴DC=5,OC=4,OB=3,
∵DC⊥y轴,x轴⊥y轴,∴DC∥BP。
∵PC∥DC,∴四边形DBPC是平行四边形。
∴DC=BP=5。∴OP=5﹣3=2。
∵2÷1=2,∴当t为2秒时,PC∥BD。
(2)∵PC⊥BC,x轴⊥y轴,∴∠COP=∠COB=∠BCP=90。
∴∠PCO+∠BCO=90°,∠CPO+∠PCO=90°。∴∠CPO=∠BCO。
∴△PCO∽△CBO。∴

,即

,解得

。
∵

÷1=

,∴当t为

秒时,PC⊥BC。
(3)设⊙P的半径是R,分为三种情况:
①当⊙P与直线DC相切时,
如图1,过P作PM⊥DC交DC延长线于M,

则PM=OC=4=OP,
∵4÷1=4,∴t=4秒。
②如图2,当⊙P与BC相切时,

∵∠BOC=90°,BO=3,OC=4,∴由勾股定理得:BC=5。
∵∠PMB=∠COB=90°,∠CBO=∠PBM,∴△COB∽△PBM。
∴

,即

,解得R=12。
∵12÷1=12,∴t=12秒。
③如图3,当⊙P与DB相切时,

根据勾股定理得:

,
∵∠PMB=∠DAB=90°,∠ABD=∠PBM
∴△ADB∽△MPB。
∴

,即

,解得

。
∵(

)÷1=

,∴t

秒。
综上所述,当⊙P与△BCD的边(或边所在的直线)相切时,t=4秒或12秒或t=

秒。

 ,即
,即 ,解得
,解得 。
。 ÷1=
÷1= ,∴当t为
,∴当t为 秒时,PC⊥BC。
秒时,PC⊥BC。

 ,即
,即 ,解得R=12。
,解得R=12。
 ,
, ,即
,即 ,解得
,解得 。
。 )÷1=
)÷1= ,∴t
,∴t 秒。
秒。 秒。
秒。 ,求出
,求出 即可。
即可。