
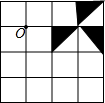
 (1)如图,首先画出其中阴影所组成的图形绕点O按顺时针方向旋转90°后的图形A;然后把所画的图形向右平移一格,再向上平移一格得到图形B.
(1)如图,首先画出其中阴影所组成的图形绕点O按顺时针方向旋转90°后的图形A;然后把所画的图形向右平移一格,再向上平移一格得到图形B. 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:阅读理解
| 61 |
| 61 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)如图,首先画出其中阴影所组成的图形绕点O按顺时针方向旋转90°后的图形A;然后把所画的图形向右平移一格,再向上平移一格得到图形B.
(1)如图,首先画出其中阴影所组成的图形绕点O按顺时针方向旋转90°后的图形A;然后把所画的图形向右平移一格,再向上平移一格得到图形B.查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:044
(1)如图,首先画出其中阴影所组成的图形绕点O按顺时针方向旋转90°后的图形;然后把所画的图形向右平移一格,再向上平移一格.
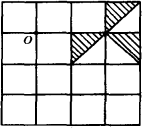
(2)设每个小正方形的面积为1,写出(1)中至最后所展现出的图形内所有阴影部分的面积和.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏南京市玄武区九年级第一学期期末考试数学试卷(解析版) 题型:解答题
阅读下列材料:
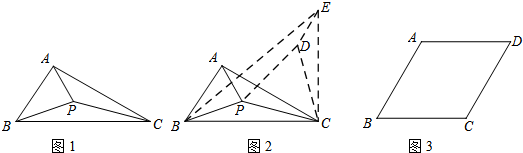
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.

小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com