
分析 (1)根据A=2x2-9x-11,B=3x2-6x+4,可以求得A-B的值;
(2)根据A=2x2-9x-11,B=3x2-6x+4,可以求得$\frac{1}{2}$A+2B的值.
解答 解:(1)∵A=2x2-9x-11,B=3x2-6x+4,
∴A-B
=2x2-9x-11-3x2+6x-4
=-x2-3x-15;
(2)∵A=2x2-9x-11,B=3x2-6x+4,
∴$\frac{1}{2}A+2B$
=$\frac{1}{2}$(2x2-9x-11)+2(3x2-6x+4)
=x2-4.5x-5.5+6x2-12x+8
=7x2-16.5x+2.5.
点评 本题考查整式的加减,解题的关键是明确整式的加减的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
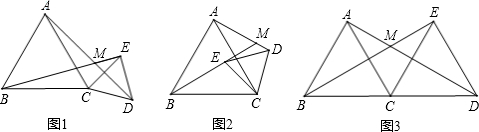
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB1C1的位置,连接BC1并延长交AB1于点D,则BD的长为$\sqrt{3}$.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB1C1的位置,连接BC1并延长交AB1于点D,则BD的长为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
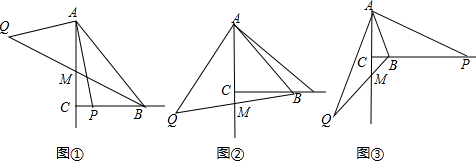
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com