解:(1)证明:∵正方形ABCD的对角线AC、BD交于点O
∴∠BOC=90°,∠OBC=∠OCD=45°,OB=OC,.AB=BC=DC=AD.
∵∠EOF=90°
∵∠BOM+∠MOC=90°,
∠NOC+∠MOC=90°
∴∠BOM=∠CON.
在△OBM和△OCN中,
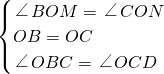
,
△OBM≌△OCN(ASA).
∴OM=ON;
(2)∵△OBM≌△OCN,
∴S
△OBM=S
△OCN.
∴S
△OBM+S
△MOC=S
△OCN+S
△MOC,
即S
△OBC=S
四边形MONC.
∵S
△OBC=4×4×

=4,
∴S
四边形MONC=4;
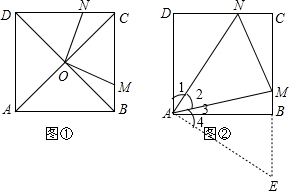
(3)绕点A顺时针旋转△ADN90°得到△ABE,
∴△ABE≌△ADN,
∴∠4=∠1.AE=AN,BE=DN.
∵∠2=45°,
∴∠1+∠3=45°.
∵∠4+∠3=∠MAE=45°.
∴∠MAE=∠2.
在△ANM和△AEM中,
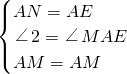
,
∴△ANM≌△AEM(SAS),
∴MN=ME=MB+BE,
∴MN=DN+MB.
∵C
△MNC=MN+MC+CN,
∴C
△MNC=DN+MB+MC+CN=DC+BC=2BC.
∵C正方形ABCD=AB+BC+CD+AD=4BC.
∴△MCN的周长等于正方形ABCD周长的一半.
分析:(1)由正方形的性质可以得出△BOM≌△CON,由全等三角形的性质就可以得出ON=OM;
(2)由全等可以得出S
△BOM=S
△CNF,就可以得出S
四边形MONC=S
△BOC,S
△BOC的面积就可以得出结论;
(3)绕点A顺时针旋转△ADN90°得到△ABE,得出△ABE≌△ADN,由全等三角形的性质可以得出△ANM≌△AEM,进而有MN=ME=MB+BE,分别表示出C
△MNC=DN+MB+MC+CN=DC+BC=2BC.C
正方形ABCD=AB+BC+CD+AD=4BC.从而可以得出结论.
点评:本题考查了正方形的性质的运用,三角形的周长和正方形的周长的运用,全等三角形的判定及性质的运用,旋转的性质的运用,解答时证明三角形全等得出OM=ON是关键.

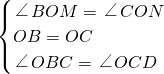 ,
,
 =4,
=4,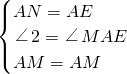 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
