
分析 (1)先将括号内的式子通分,再将除法转化为乘法,然后约分计算即可;
(2)根据一元二次方程的定义以及根的判别式得到k≠0且△>0,即22-4×k×(-3)>0,然后解两个不等式即可得到k的取值范围.
解答 解:(1)原式=($\frac{1}{x+2}$-$\frac{x+2}{x+2}$)•$\frac{x+2}{(1+x)(1-x)}$
=-$\frac{1+x}{x+2}$•$\frac{x+2}{(1+x)(1-x)}$
=-$\frac{1}{1-x}$;
(2)∵关于x的一元二次方程kx2+2x-3=0有两个不相等的实数根,
∴k≠0,且△>0,即22-4×k×(-3)>0,
解得k>-$\frac{1}{3}$且k≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程ax2+bx+c=0(a≠0)的定义以及分式的混合运算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
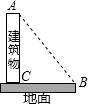 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.334×1011 | B. | 3.34×1010 | C. | 3.34×109 | D. | 3.34×102 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
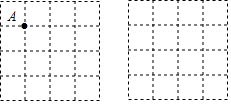 如图,正方形网格的每个下正方形的边长均为1,每个小正方形的顶点叫做格点.
如图,正方形网格的每个下正方形的边长均为1,每个小正方形的顶点叫做格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,请分别仅用一把无刻度的直尺画图:
如图,在正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,请分别仅用一把无刻度的直尺画图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com