
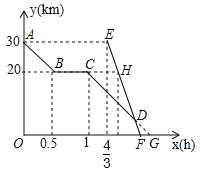
����Ŀ����ĩ��С�������г��Ӽҳ�����Ұ�⽼�Σ��Ӽҳ���0.5Сʱ����أ�����һ��ʱ���ԭ��ǰ���ҵأ�С�����1Сʱ20���Ӻ�����ݳ�����ͬ·��ǰ���ҵأ���ʻ10����ʱ��ǡ�þ����أ���ͼ�����Ǿ��ҵص�·��y��km����С�����ʱ��x��h���ĺ���ͼ��
��1��С���ﳵ���ٶ�Ϊ km/h��H������ ��
��2��С���Ӽҳ�������Сʱ�������ϣ���ʱ��ҵ�·�̶�Զ��
��3����������������С�������г�ͬʱ�����ҵأ��˴˽���ʱ����Բ��ƣ�����С����Ԥ��ʱ���缸���ӵ����ҵأ�

���𰸡���1��20��H��![]() ��20������2��С������1.75Сʱ�������ϣ���ʱ���25km����3��10��
��20������2��С������1.75Сʱ�������ϣ���ʱ���25km����3��10��
�������������������1�����ݺ���ͼ�е����ݣ���С���Ӽҵ��ص�·�̺�ʱ��������С���ﳵ���ٶȣ�
��2�������ֱ��AB�Ľ���ʽ���ٸ���ֱ��AB��CD�����ֱ��CD�Ľ���ʽ�������ֱ��EF�Ľ���ʽ������ֱ��CD��ֱ��EF�Ľ���ʽ���������D�����꼴�ɣ�
��3����y=0���ֱ����ֱ��CD��ֱ��EF�Ľ���ʽ���ֱ���������y=0ʱ��ĺ����꣬�������������IJ�ֵ���ɣ�
�����������1���ɺ���ͼ���Եó���С���Ҿ���ص�·��Ϊ10km������ʱ��Ϊ0.5h����С���ﳵ���ٶ�Ϊ��10��0.5=20��km/h����������ɵó�����H��������Ϊ20��������Ϊ�� ![]() =
=![]() ���ʵ�H������Ϊ��
���ʵ�H������Ϊ��![]() ��20����
��20����
��2����ֱ��AB�Ľ���ʽΪ��y1=k1x+b1������A��0��30����B��0.5��20������ã�y1=��20x+30����AB��CD������ֱ��CD�Ľ���ʽΪ��y2=��20x+b2������C��1��20������ã�b2=40����y2=��20x+40����ֱ��EF�Ľ���ʽΪ��y3=k3x+b3������E��![]() ��30����H��
��30����H��![]() ��20������ã�k3=��60��b3=110����y3=��60x+110���ⷽ����
��20������ã�k3=��60��b3=110����y3=��60x+110���ⷽ����![]() ����
����![]() ������D����Ϊ��1.75��5����30��5=25��km��������С������1.75Сʱ�������ϣ���ʱ���25km��
������D����Ϊ��1.75��5����30��5=25��km��������С������1.75Сʱ�������ϣ���ʱ���25km��
��3����y=0����ֱ��CD����ʽ�У���20x+40=0�����x=2����y=0����ֱ��EF�Ľ���ʽ�У���60x+110=0�����x=![]() ��2��
��2��![]() =
=![]() ��h��=10�����ӣ�����С����Ԥ��ʱ����10���ӵ����ҵأ�
��h��=10�����ӣ�����С����Ԥ��ʱ����10���ӵ����ҵأ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.a+a2=2a3
B.a2a3=a6
C.��2a4��4=16a8
D.����a��6��a3=a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͳ��ͼ��������ͼ��������ͼ��������ͼ����ֱ��ͼ.�ĸ��ص㣺��a�����ڱȽ�����֮��IJ��죻��b��������ʾ����֮���Ƶ���IJ����c��������ʾ���ݵı仯���ƣ���d��������ʾÿ����������������Ĵ�С.ͳ��ͼ���ص�ѡ�䷽���ֱ��ǣ�������a����������c����������d����������b��. ����ѡ�䷽����ȷ���У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ���꼶400��ѧ����������������г����50��ѧ�������ؽ���ͳ�Ʒ���������������У�������ָ
A. 400��ѧ�� B. ����ȡ��50��ѧ��
C. 400��ѧ�������� D. ����ȡ��50��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�22��)Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
��1����y��x�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�B���������������35�ã���������A���������������ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ߺ������������й�������Ĺ�·����·�������������Ų��õ���б�������ͣ����ͼ����ͼ���Ǵ�ͼ���������ƽ��ͼ��������վ�����ϲ������AB��ˮƽ����ļн���30�㣬����CD��ˮƽ����ļн���60�㣬���������˵ľ���BCΪ2�ף��������˾���ADΪ20�ף����������BH�ij����������ȷ��0.1�ף�![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ��O��OE��AB��OF��CD��
(1)ͼ�����COE�����Ľ���___________________�� (�ѷ��������ĽǶ�д����)
(2)�����AOC =![]() ��EOF �����AOC�Ķ�����
��EOF �����AOC�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com