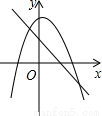【答案】
分析:根据二次函数的开口方向确定出a的正负情况,再根据二次函数的对称轴确定出b的正负情况,再根据一次函数图象确定a、b的正负情况,如果两个函数的a、b的正负情况一致,则正确,否则不正确.
解答:解:A、∵二次函数图象开口向下,
∴a<0,
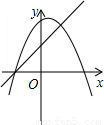
又∵对称轴x=-
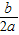
>0,
∴b>0,
根据一次函数图象,a<0,b>0,故本选项正确;
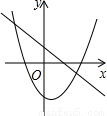
B、∵二次函数图象开口向上,
∴a>0,
又∵对称轴x=-
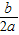
>0,
∴b<0,
根据一次函数图象,a<0,b>0,故本选项错误;
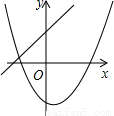
C、∵二次函数图象开口向上,
∴a>0,
又∵对称轴x=-
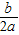
>0,
∴b<0,
根据一次函数图象,a>0,b>0,故本选项错误;
D、∵二次函数图象开口向下,
∴a<0,
又∵对称轴x=-
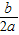
>0,
∴b>0,
根据一次函数图象,a>0,b>0,故本选项错误.
故选A.
点评:本题考查了二次函数图象,一次函数图象,根据函数图象确定出系数的正负情况是解题的关键.

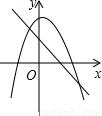


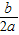 >0,
>0,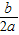 >0,
>0,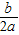 >0,
>0,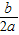 >0,
>0,