
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先根据勾股定理的逆定理对①④中△ABC的形状进行判断;再根据三角形的内角和是180°对②③中△ABC的形状作出判断即可.
解答 解:①∵△ABC中,a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$,
∴b2+c2≠a2,
∴△ABC不是直角三角形;
②∵△ABC中,∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∵∠A+∠B+∠C=180°,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=2×30°=90°,
∴△ABC是直角三角形;
③∵△ABC中,∠A=36°,∠C=54°,
∴∠B=90°,
∴△ABC是直角三角形;
④∵△ABC中,a=1,b=2$\sqrt{2}$,c=3,
∴12+(2$\sqrt{2}$)2=9=32,即a2+b2=c2,
∴△ABC是直角三角形.
故选C.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,可利用勾股定理的逆定理和直角三角形的定义判断.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9π | B. | 16π | C. | 27π | D. | 36π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
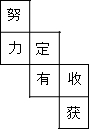 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )| A. | 定 | B. | 有 | C. | 收 | D. | 获 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=b | B. | a=c | C. | a=2b=c | D. | b=c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com