练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

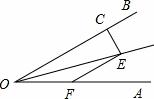
    如图∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=1，则EF=      ．


    2

    【解析】

    试题分析：作EG⊥OA于F，根据角平分线的性质得到EG的长度，再根据平行线的性质得到∠OEF=∠COE=15°，然后利用三角形的外角和内角的关系求出∠EFG=30°，利用30°角所对的直角边是斜边的一半解题．

    试题解析：作EG⊥OA于G，

    ∵EF∥OB，

    ∴∠OEF=∠COE=15°，

    ∵∠AOE=15°，

    ∴∠EFG=15°+15°=30°，

    ∵EG=CE=1，

    ∴EF=2×1=2．

    【难度】一般


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    .已知某开发区有一块四边形的空地ABCD，如图所示，现计划在该空地上种草皮，经测量，∠A＝90°，AB＝3m，BC＝12m，CD＝13m，DA＝4m，若每平方米草皮需200元，问：需要投入多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1＋∠2＋∠3＋∠4＋∠5＝        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，由全等三角形拼出的一系列图形中，第n个图形由n+1个全等三角形拼成，则第4个图形中平行四边形的个数为             ；第2n－1个图形中平行四边形的个数为             ．

      ……

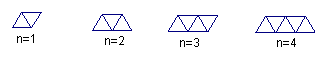    查看答案和解析>>

    科目：初中数学 来源： 题型：


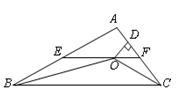
    如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：

    ①∠BOC＝90º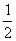＋∠A；

    ②EF=BE+CF；

    ③设OD＝m，AE＋AF＝n，则S△AEF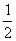＝mn；

    ④EF是△ABC的中位线．

    其中正确的结论是              ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，菱形ABCD的对角线AC上有一动点P，BC=6，∠ABC=150°，则线段AP＋BP＋PD的最小值为               ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．已知函数是反比例函数，则m         ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


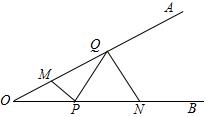
    如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是_________．

    查看答案和解析>>

    同步练习册答案