
 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )| A. | DF⊥AB | B. | CG=2GA | C. | CG=DF+GE | D. | S四边形BFGC=$\sqrt{3}$-1 |
分析 A、由四边形ABCD是菱形,得出对角线平分对角,求得∠GAD=∠2,得出AG=GD,AE=ED,由SAS证得△AFG≌△AEG,得出∠AFG=∠AEG=90°,即可得出A正确;
B、由DF⊥AB,F为边AB的中点,证得AD=BD,证出△ABD为等边三角形,得出∠BAC=∠1=∠2=30°,由AC=2AB•cos∠BAC,AG=$\frac{AF}{cos∠BAC}$,求出AC,AG,即可得出B正确;
C、由勾股定理求出DF=$\sqrt{A{D}^{2}-A{F}^{2}}$,由GE=tan∠2•ED求出GE,即可得出C正确;
D、由S四边形BFGC=S△ABC-S△AGF求出数值,即可得出D不正确.
解答 解:∵四边形ABCD是菱形,
∴∠FAG=∠EAG,∠1=∠GAD,AB=AD,
∵∠1=∠2,
∴∠GAD=∠2,
∴AG=GD,
∵GE⊥AD,
∴GE垂直平分AD,
∴AE=ED,
∵F为边AB的中点,
∴AF=AE,
在△AFG和△AEG中,$\left\{\begin{array}{l}{AF=AE}\\{∠FAG=∠EAG}\\{AG=AG}\end{array}\right.$,
∴△AFG≌△AEG(SAS),
∴∠AFG=∠AEG=90°,
∴DF⊥AB,
∴A正确;
∵DF⊥AB,F为边AB的中点,
∴AF=$\frac{1}{2}$AB=1,AD=BD,
∵AB=AD,
∴AD=BD=AB,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠BAC=∠1=∠2=30°,
∴AC=2AB•cos∠BAC=2×2×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
AG=$\frac{AF}{cos∠BAC}$=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$,
∴CG=AC-AG=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴CG=2GA,
∴B正确;
∵GE垂直平分AD,
∴ED=$\frac{1}{2}$AD=1,
由勾股定理得:DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
GE=tan∠2•ED=tan30°×1=$\frac{\sqrt{3}}{3}$,
∴DF+GE=$\sqrt{3}$+$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$=CG,
∴C正确;
∵∠BAC=∠1=30°,
∴△ABC的边AC上的高等于AB的一半,即为1,
FG=$\frac{1}{2}$AG=$\frac{\sqrt{3}}{3}$,
S四边形BFGC=S△ABC-S△AGF=$\frac{1}{2}$×2$\sqrt{3}$×1-$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$-$\frac{\sqrt{3}}{6}$=$\frac{5\sqrt{3}}{6}$,
∴D不正确;
故选:D.
点评 本题考查了菱形的性质、全等三角形的判定与性质、勾股定理、三角函数、线段垂直平分线的性质、含30°角的直角三角形的性质等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:选择题
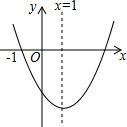 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>-1时,y<0 | C. | b=2a | D. | 9a+3b+c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.
△AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.
如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校九年级进行了体育模拟测试,现从中随机抽取了部分学生的体育成绩进行分段(A:50分;B:49-45分;C:44-40;D:39-35;E:34-0),已知C等级人数占20%,其他结果在统计图中显示.回答下列问题:
某校九年级进行了体育模拟测试,现从中随机抽取了部分学生的体育成绩进行分段(A:50分;B:49-45分;C:44-40;D:39-35;E:34-0),已知C等级人数占20%,其他结果在统计图中显示.回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com