解:(1)直线y=-x+3中,
当x=0时,y=3;当y=0时,x=3;
故C(0,3),B(3,0).
代入抛物线的解析式中,可得:

,
解得
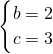
;
∴该抛物线的解析式为:y=-x
2+2x+3,
由于y=-x
2+2x+3=-(x-1)
2+4,
故顶点坐标为(1,4).
(2)若△QAC的周长最小,那么QA+QC最小;
由题意知:A、B关于抛物线的对称轴对称,
所以直线BC与抛物线对称轴的交点即为所求的Q点;
则有:

,
解得
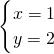
;
故Q(1,2).
(3)由于△PAC、△PAB等高,则它们的面积比等于底边的比,
所以PB=3PC;
设P(a,-a+3),分三种情况考虑:
①当a<0时,P点位于BC的延长线上;

过P作PM⊥x轴于M,则有:BM=PM=3-a;
∵PM⊥x轴,CO⊥x轴,
∴PM∥CO,即△BCO∽△BPM;
得:

=

,
∵OC=OB=3,
∴a=-1.5,PM=BM=4.5;
故P(-1.5,4.5);
②当0≤a≤3时,P点位于线段BC上;
同①可求得点P(

);
③当a>3时,P点位于CB的延长线上,此时PC>PB,此种情况不成立.
综上所述,点P的坐标为(-1.5,4.5)或(

).
分析:(1)根据直线BC的解析式,即可求出B、C两点的坐标,将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值,从而确定该抛物线的解析式,然后将所得的解析式化为顶点坐标式,即可得到该抛物线的顶点坐标.
(2)由于AC的长为定值,若△QAC的周长最小,那么QA+QC的值最小;已知A、B关于抛物线的对称轴对称,那么所求的点Q必为直线BC与抛物线对称轴的交点,已知了直线BC的解析式,联立抛物线的对称轴方程,即可求得点Q的坐标.
(3)由于△PAC、△PAB同高不等底,那么它们的面积比等于底长的比,即PB=3PC,设出点P点坐标P(a,-a+3),因此:
①当P在BC延长线上,即a<0时,过P作PM⊥x轴于M,易证得△BCO∽△BPM,根据BC、PB的比例关系,即可求出PM、BM的值,从而确定P点的坐标;
②当P在线段BC上,即0<a<3时,解法同上;
③当P在CB延长线上,即a>3时,此时PC>PB,显然不符合题意,因此此种情况不成立.
综合上面三种情况即可求得符合条件的P点坐标.
点评:此题是二次函数的综合题,涉及到函数图象与坐标轴交点坐标的求法、二次函数解析式的确定、平面展开-最短路径问题、相似三角形的判定和性质、图象面积的求法等重要知识.(3)题中,能够将三角形的面积关系,转化为线段的比例关系,是解决问题的关键.

 是抛物线与x轴的另一个交点.
是抛物线与x轴的另一个交点. ,
,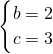 ;
; ,
,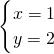 ;
;
 =
= ,
, );
); ).
).

 口算题天天练系列答案
口算题天天练系列答案
 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=