练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点，点0为坐标原点，则S△AOB=4．

    分析 求出OA、OB的值，根据三角形面积公式求出即可．

    解答 解：把x=0代入y=-$\frac{1}{2}$x+2得：y=2，
    把y=0代入y=-$\frac{1}{2}$x+2得：x=4，
    即OA=4，OB=2，
    S△AOB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$×4×2=4，
    故答案为：4．

    点评 本题考查了一次函数图象上点的坐标特征的应用，关键是求出OA、OB的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．解方程：
    （1）（x-2）（x-5）=0
    （2）2x2+12x-6=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在正方形ABCD中，点E，F在对角线BD上，若再添加一个条件，就可证出AE=CF．
    （1）你添加的条件是BE=DF．
    （2）请你根据题目中的条件和你添加的条件证明AE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．探究发散：
    （1）填空：
    ①$\sqrt{{3}^{2}}$=3；②$\sqrt{0．{5}^{2}}$=0.5；③$\sqrt{（-6）^{2}}$=6；
    ④$\sqrt{{0}^{2}}$=0；⑤$\sqrt{（-\frac{3}{4}）^{2}}$=$\frac{3}{4}$；⑥$\sqrt{（-\frac{1}{3}）^{2}}$=$\frac{1}{3}$．
    （2）根据计算结果回答：$\sqrt{{a}^{2}}$一定等于a吗？你发现其中的规律了吗？请你用自己的语言描述出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．将公式$\frac{1}{R}$=$\frac{1}{{R}_{1}}$$+\frac{1}{{R}_{2}}$（R，R1，R2均不为零，且R≠R2）变形成求R1的式子，正确的是（　　）
    A．R1=$\frac{R{R}_{2}}{{R}_{2}-R}$B．R1=$\frac{R{R}_{2}}{{R}_{2}+R}$C．R1=$\frac{R{R}_{1}+R{R}_{2}}{{R}_{2}}$D．R1=$\frac{R{R}_{2}}{R-{R}_{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

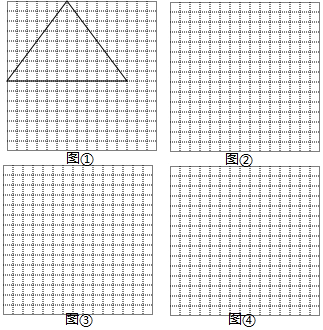    11．如图，在15×15的网格中，每个小正方形的边长均为1，每个小格的顶点叫做格点，图①中的三角形是以格点为顶点，边长都为整数的锐角三角形．
    在图②③④中分别画出一个以格点为顶点，边长都为整数的锐角三角形，并在每条边上标出其长度（图①-④中的三角形互不全等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．计算：（-2）2016+（-2）2017所得的结果是（　　）
    A．-2B．2C．-22016D．22016

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

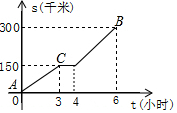    15．杨师傅开车从A地出发去300千米远的B地游玩，其行驶路程s与时间t之间的关系如图所示，出发一段时间后，汽车发生故障，需停车检修，修好后又继续行驶．根据题意回答下列问题：
    （1）上述问题中反映的是哪两个变量之间的关系？并指出自变量和因变量；
    （2）汽车停车检修了多长时间？修车的地方离B地还有多远？
    （3）车修好后每小时走多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．解不等式组$\left\{\begin{array}{l}{x+6≥4x-3}\\{\frac{2x+5}{3}-2＞1-x}\end{array}\right.$，并求它的整数解．

    查看答案和解析>>

    同步练习册答案