练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．（1）分解因式：6xy2-12x2y3
    （2）分式计算：$\frac{x-5}{4-x}$-1-$\frac{1}{x-4}$．

    分析 （1）根据提公因式法，可得答案；
    （2）根据通分，可得同分母分式，根据同分母分式的加减，可得答案．

    解答 解：（1）原式=6xy2（1-2xy）；
    （2）原式=$\frac{5-x}{x-4}$-$\frac{x-4}{x-4}$-$\frac{1}{x-4}$=$\frac{5-x-x+4-1}{x-4}$=$\frac{2（4-x）}{x-4}$=-2．

    点评 本题考查了分式的加减，通分化成同分母分式的加减是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．把下列各式因式分解：
    （1）（x+1）2-4x；
    （2）（m+n）3-4（m+n）；
    （3）（x+1）（x-1）-3；
    （4）（x+2）（x+3）+$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列各式的分解因式中，没有用到公式法的是（　　）
    A．3m2-6mn+3n2=3（m-n）2B．x2b+ab2+ab=ab（a+b+1）
    C．mx2-4m=m（x-2）（x+2）D．x2+12x+36=（x+6）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）已知|ab+2|与|b-1|互为相反数，求a-b的值？
    （2）计算：2x2-5x+x2+4x-3x2+2，先化简，再求值，其中x=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．解方程：x2-8x-9=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

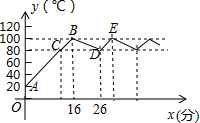    7．张老师办公室的饮水机具有自动调节功能，开机后自动进行加热状态，水温y（℃）与开机后用时x（分钟）成一次函数关系，当水温上升到100℃时停止加热，水温开始下降，此时水温y（℃）与开机后用时x（分钟）仍成一次函数某天早晨7：00时，张老师打开饮水机，水温变化情况如图所示．
    （1）求线段AB的函数解析式；
    （2）①开机后经过多少时间，水温第一次达到80℃？
    ②求开机后经过多少时间，水温第二次达到100℃？
    （3）当张老师8：45时回到办公室，请直接写出此时饮水机内的水温．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知$\frac{a}{b+c+d}$=$\frac{b}{a+c+d}$=$\frac{c}{a+b+d}$=$\frac{d}{a+b+c}$=k，则k的值为（　　）
    A．-1B．3C．-1或$\frac{1}{3}$D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知四条线段a，b，c，d．若有$\frac{a}{b}$=$\frac{c}{d}$（或a：b=c：d），则线段a，b，c，d是成比例线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
    例如，由1，可得等式：（a+2b）（a+b）=a2+3ab+2b2
    （1）如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．
    （2）利用（1）中所得到的结论，解决下面的问题：
    已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值．
    （3）如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．

    查看答案和解析>>

    同步练习册答案