34、关于图形变化的探讨:
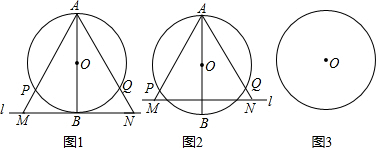
(1)①例题1.如图1,AB是⊙O的直径,直线l与⊙O有一个公共点C,过A、B分别作l的垂线,垂足为E、F,则EC=CF.
②上题中,当直线l向上平行移动时,与⊙O有了两个交点C
1、C
2,其它条件不变,如图2,经过推证,我们会得到与原题相应的结论:EC
1=C
2F.
③把直线1继续向上平行移动,使弦C
1C
2与AB交于点P(P不与A,B重合).在其它条件不变的情况下,请你在图3的圆中将变化后的图形画出来,标好对应的字母,并写出与①②相应的结论等式.判断你写的结论是否成立,若不成立,说明理由,若成立,给以证明.结论
EC1=C2F
.证明结论成立或说明不成立的理由
(2)①例题2.如图4,BC是⊙O的直径.直线1是过C点的切线.N是⊙O上一点,直线BN交1于点M.过N点的切线交1于点P,则PM
2=PC
2.
②把例题2中的直线1向上平行移动,使之与⊙O相交,且与直线BN交于B、N两点之间.其它条件仍然不变,请你利用图5的圆把变化后的图形画出来,标好相应的字母,并写出与①相应的结论等积式,判断你写的结论是否成立,若不成立,说明理由,若成立,给以证明.结论
PM2=PC1•PC2
.证明结论成立或说明不成立的理由:
(3)总结:请你通过(1)、(2)的事实,用简练的语言,总结出某些几何图形的一个变化规律
在某些几何图形中,平行移动某条直线,有些几何关系保持不变.
.