
����Ŀ����ͼ����Rt��ABC�У���B=Rt��,ֱ�DZ�AB��BC�ij�(AB��BC)�Ƿ���![]() 2��7
2��7![]() ��12��0������������P�ӵ�A��������ÿ��1����λ���ٶ�����ABC�� A��B��C��A�ķ����˶����˶�ʱ��Ϊt(��)��
��12��0������������P�ӵ�A��������ÿ��1����λ���ٶ�����ABC�� A��B��C��A�ķ����˶����˶�ʱ��Ϊt(��)��
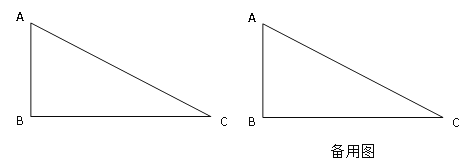
��1����AB��BC�ij���
��2������P�˶�����BC��ʱ�������ʹAP��Ϊ![]() ʱ�˶�ʱ��t��ֵ��
ʱ�˶�ʱ��t��ֵ��
��3����P���˶��Ĺ��������Ƿ���ڵ�P��ʹ��ABP�ǵ��������Σ������ڣ�������˶�ʱ��t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��AB��3��BC��4��2��t��4ʱ��AP��![]() ��3����tΪ9���9.5���6 (��)��
��3����tΪ9���9.5���6 (��)��![]() (��)ʱ����ABP�ǵ���������.
(��)ʱ����ABP�ǵ���������.
�������������������1���ⷽ��x2��7x��12��0 ���ɵ�AB��BC�ij���
��2���ɡ�ABP��ֱ�������θ��ݹ��ɶ����ɵõ�BP�ij����Ӷ��õ��˶���ʱ�䣻
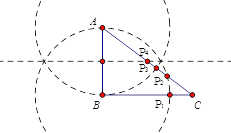
��3���ֱ���A��BΪԲ�ģ���AB��Ϊ�뾶��Բ��Բ��BC��AC�Ľ��㼴Ϊ�����P�㣬����AB���д��ߣ��д�����AC�Ľ���Ҳ�������P�㣬�Ӷ��ɵ��˶�ʱ��.
�����������1����x2��7x��12��(x��3)(x��4)��0
��![]() ��3��
��3��![]() ��4��
��4��
��AB��3��BC��4
��2���������![]()
��![]() ��
�� ![]() (��ȥ)
(��ȥ)
��t��4ʱ��AP��![]()
��3�����ڵ�P��ʹ��ABP�ǵ���������.
����AP��AB��3ʱ�� t=9(��).
����BP��BA��3ʱ����p��AC��ʱ�� t=![]() (��)
(��)
��p��BC��ʱ�� t=6(��)
����BP=AP (��PΪAC�е�ʱ)��
��t��9.5(��)
��֪��tΪ9���9.5���6 (��)��![]() (��)ʱ����ABP�ǵ���������.
(��)ʱ����ABP�ǵ���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ⷢչҪ������������2014����2017�깲Ͷ��20.93��Ԫ��ȫ������ѧУ����ȫ����죬20.93���ÿ�ѧ��������ʾΪ��������
A. 20.93��108 B. 2.093��109 C. 2.093��108 D. 0.2093��1010
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڵ�ʽ10(x��3)��3(x��3)������ͬ����(x��3)�ͻ�õ�10��3������֪��10��3����ô�ɴ˿��Բ²�x��3��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
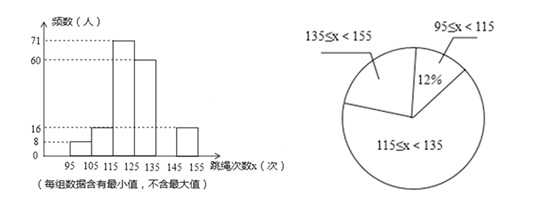
����Ŀ�������ؿ�չ��������������������У�Ϊ���˽����ѧ��������Ŀ�չ�������������ȫ�����꼶����ͬѧ1���������Ĵ����������������ͳ�ƣ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
��1�����ι�����˶�����ѧ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��ȱ���֣�ֱ��д������ͳ��ͼ������������Χ135��x��155�������ε�Բ�ĽǶ�����
��3�������γ���У�����������125�����ϣ���125�Σ�Ϊ���㣬�������ȫ��8000������ѧ�����ж�����ѧ���ijɼ�Ϊ���㣿
��4���������������Ϣ,�����п�չ��ѧ�������̸̸�Լ��Ŀ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ƽ�������ĵ�����ȣ���������ǣ� ��
A. 1 B. -1 C. ��1 D. ��1��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
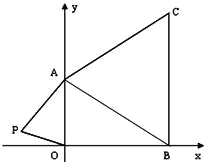
����Ŀ����ͼ��������ֱ������ϵ�У���֪A��0��a����B��b��0����C��b��c�����㣬����a��b��c�����ϵʽ![]()
��1����a��b��c��ֵ��
��2������ڵڶ���������һ��P��m�� ![]() �������ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
�������ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
��3���ڣ�2���������£��Ƿ���ڵ�P��ʹ�ı���ABOP�����Ϊ��ABC�������ȣ������ڣ������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס���������ֱ��������ABCD�Ķ���A��Cͬʱ�������εı߿�ʼ�ƶ�������˳ʱ�뷽���У��ҵ�����ʱ�뷽���У������ٶ����ҵ��ٶȵ�3���������ǵ�2015���������������ϣ� ��
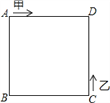
A. AB B. BC C. CD D. DA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ��������ȫƽ����ʽ���ǣ���
A.��3x��y������y��3x��
B.��3x��y����3x+y��
C.����3x��y����y��3x��
D.����3x��y����y+3x��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com