
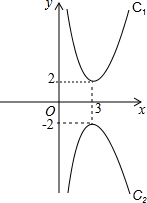
 如图,在同一平面直角坐标系中,画出抛物线C1:y=(x-3)2+2和它关于x轴对称的抛物线C2,我们容易发现,抛物线C2的开口向下,形状与抛物线C1相同,其解析式是y=-(x-3)2-2,请运用轴对称的知识,求出抛物线C1关于y轴对称的抛物线C3的解析式.
如图,在同一平面直角坐标系中,画出抛物线C1:y=(x-3)2+2和它关于x轴对称的抛物线C2,我们容易发现,抛物线C2的开口向下,形状与抛物线C1相同,其解析式是y=-(x-3)2-2,请运用轴对称的知识,求出抛物线C1关于y轴对称的抛物线C3的解析式.  Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
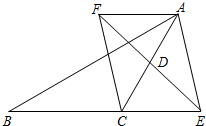 如图,在△ABC中,AC=BC,∠BAC=30°,D是EF的中点,E是线段BC延长线上一点,过点A作AF∥BE,与线段ED的延长线交于点F,连结AE、CF.
如图,在△ABC中,AC=BC,∠BAC=30°,D是EF的中点,E是线段BC延长线上一点,过点A作AF∥BE,与线段ED的延长线交于点F,连结AE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
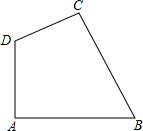 如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${x^2}+\frac{1}{x^2}$=0 | B. | (x-1)x=1 | C. | ax2+bx=0 | D. | x2-xy-y2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
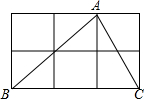 如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有3个(不含△ABC).
如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有3个(不含△ABC).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com