
【小题1】探究 (1)在图①中,已知线段AB、CD,点E、F分别为线段AB、CD的中点.
①若A(-2,0),B(4,0),则E点的坐标为 ;
②若C(-3,3),D(-3,-1),则F点的坐标为 ;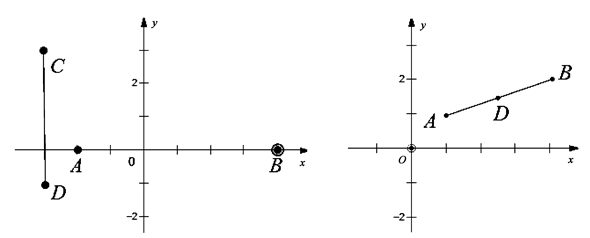
图① 图②
【小题2】在图②中,已知线段AB的端点坐标为A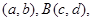 求出图中AB的中点D的坐标(用含
求出图中AB的中点D的坐标(用含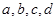 的代数式表示),并给出求解过程.
的代数式表示),并给出求解过程.
归纳无论线段AB处于指定坐标系中的哪个位置,当其端点坐标为A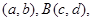 AB中点为
AB中点为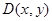 时,
时, ,
, 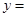 .(不必证明)
.(不必证明)
运用已知如图③,一次函数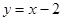 与反比例函数
与反比例函数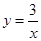 的图象交点为A,B.
的图象交点为A,B.
①求出交点A,B的坐标;
②若以A,O,B,P为顶点的四边形
是平行四边形,请利用上面的结论求出顶点P的坐标]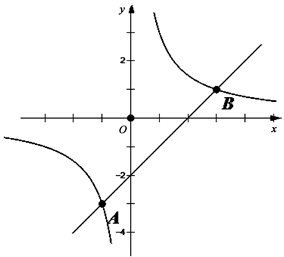
【小题1】探究(1)①(1,0)②(-3,1)……1分
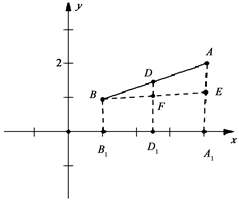
【小题2】如图4,过点A,D,B三点分别作x轴的垂线,垂足分别为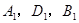 ,
,
则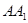 ‖
‖ ‖
‖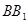 ,过B点作BE‖
,过B点作BE‖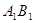 ,可得四边形
,可得四边形 为矩形,四边形
为矩形,四边形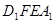 为矩形,………… 2分
为矩形,………… 2分
∵D为线段AB的中点,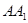 ‖
‖ ‖
‖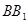 .∴F为线段BE的中点. ………………3分
.∴F为线段BE的中点. ………………3分
∴BF=EF∵四边形 为矩形,四边形
为矩形,四边形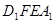 为矩形
为矩形
∴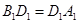
∴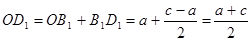 ……………4分
……………4分 即D点的横坐标是
即D点的横坐标是 .同理可得D点的纵坐标是
.同理可得D点的纵坐标是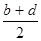 ……………5分
……………5分
归纳  ,
,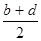 ……………6分
……………6分
运用
①由题意得: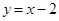 和
和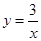 的
的
解为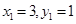 和
和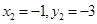 ,
,
即交点坐标为A(3,1)和
B(-1,-3). …………7分
②如图5,以AB为对角线时,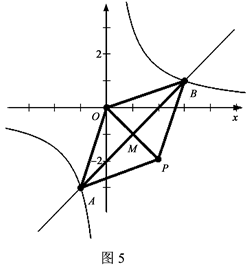
由上面的结论知AB的中点M的坐标为(1,-1).
∵平行四边形对角线互相平分,
∴OM=OP,即M为OP的中点. ∴P点坐标为(2,-2) …………8分
同理可得分别以OA,OB为对角线时,P点坐标为(-4,-4),(4,4)……9分
因此,P点坐标可能为(2,-2)、(-4,-4)、(4,4).……………………10分
解析


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与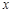 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.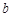 =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):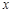 轴于点F.求FC的长;
轴于点F.求FC的长;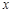 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:

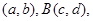 求出图中AB的中点D的坐标(用含
求出图中AB的中点D的坐标(用含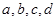 的代数式表示),并给出求解过程.
的代数式表示),并给出求解过程.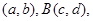 AB中点为
AB中点为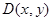 时,
时, ,
, 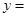 .(不必证明)
.(不必证明)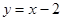 与反比例函数
与反比例函数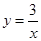 的图象交点为A,B.
的图象交点为A,B. 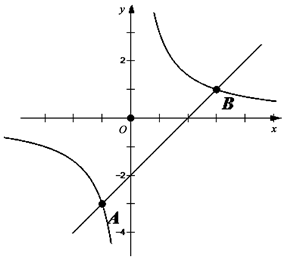
查看答案和解析>>
科目:初中数学 来源:2012届山东省德州市九年级中考模拟考试数学试卷(带解析) 题型:解答题
【小题1】探究新知
如图1,已知ΔABC与ΔABD的面积相等,试判断AB与CD的位置关系,并说明理由;[来源:
【小题2】结论应用:
如图2,过点M,N在反比例函数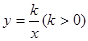 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明MN//EF。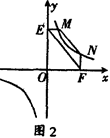
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com