
| A. | 20cm | B. | 50cm | C. | 40cm | D. | 45cm |
分析 根据题意画出示意图,AC为圆桶底面直径,AC=24cm,CB=32cm,那么线段AB的长度就是桶内所能容下的最长木棒的长度,在直角三角形ABC中利用勾股定理即可求出AB,也就求出了桶内所能容下的最长木棒的长度.
解答  解:如图,AC为圆桶底面直径,
解:如图,AC为圆桶底面直径,
∴AC=2×12=24cm,CB=32cm,
∴线段AB的长度就是桶内所能容下的最长木棒的长度,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2{4}^{2}+3{2}^{2}}$=40cm.
故桶内所能容下的最长木棒的长度为40cm.
故选C.
点评 本题考查勾股定理的实际应用,首先要正确理解题意,明白怎么放桶内所能容下的木棒最长,然后灵活利用勾股定理,难度一般.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在三角形MNQ中.
在三角形MNQ中.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
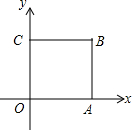 如图,在平面直角坐标系xOy中,边长为2的正方形OCBA,点A、C分别在x轴、y轴上,把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1( 0<α<90)﹒
如图,在平面直角坐标系xOy中,边长为2的正方形OCBA,点A、C分别在x轴、y轴上,把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1( 0<α<90)﹒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
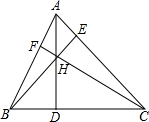 如图,AD为锐角△ABC的高线(AC>AB),H为线段AD上一点,连结BH,CH并延长分别交三角形的边于点E,F,且∠ABE=∠ACF,求证:H为△ABC的垂心.
如图,AD为锐角△ABC的高线(AC>AB),H为线段AD上一点,连结BH,CH并延长分别交三角形的边于点E,F,且∠ABE=∠ACF,求证:H为△ABC的垂心.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+8)2-9 | B. | y=(x-8)2+9 | C. | y=(x-8)2-9 | D. | y=(x+8)2+9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com