
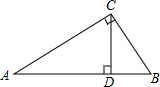
 如图,△ABC 中,∠ACB=90°,CD⊥AB于D.求证:
如图,△ABC 中,∠ACB=90°,CD⊥AB于D.求证:分析 (1)把等式左边通分,再结合勾股定理和等积法可证得结论;
(2)可证△ADC∽△CDB,利用相似三角形的性质可证得结论.
解答 证明:
(1)∵∠ACB=90°,
∴AC2+BC2=AB2,
∵CD⊥AB,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴$\frac{AB}{AC•BC}$=$\frac{1}{CD}$,
∴$\frac{A{B}^{2}}{A{C}^{2}•B{C}^{2}}$=$\frac{1}{C{D}^{2}}$,
∴$\frac{A{C}^{2}+B{C}^{2}}{A{C}^{2}•B{C}^{2}}$=$\frac{1}{C{D}^{2}}$,
∴$\frac{1}{A{C}^{2}}$+$\frac{1}{B{C}^{2}}$=$\frac{1}{C{D}^{2}}$;
(2)∵CD⊥AB于D,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠ACD+∠A=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ADC∽△CDB,
∴$\frac{AD}{CD}$=$\frac{DC}{BD}$,
∴CD2=AD•BD.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定和性质是解题的关键,注意勾股定理和等积法的应用.


科目:初中数学 来源: 题型:选择题
| A. | 检测云梦县的空气质量 | |
| B. | 孝武超市招聘,对应聘人员进行面试 | |
| C. | 调查云梦县小学生的视力和用眼卫生情况 | |
| D. | 检测梦泽鞋厂生产的鞋底能承受的弯折次数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然事件发生的概率为l | |
| B. | 不可能事件发生的概率为0 | |
| C. | 随机事件发生的概率大于等于0,小于等于1 | |
| D. | 概率很小的事件不会发生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com