
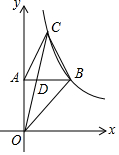
 如图,B、C两点都在反比例函数y=$\frac{k}{x}$(x>0)上,点A在y轴上,AB∥x轴,当△ABC是等边三角形时,$\frac{{S}_{△ABC}}{{S}_{△BCD}}$的值为( )
如图,B、C两点都在反比例函数y=$\frac{k}{x}$(x>0)上,点A在y轴上,AB∥x轴,当△ABC是等边三角形时,$\frac{{S}_{△ABC}}{{S}_{△BCD}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 设点B的坐标为(m,$\frac{k}{m}$),则点C的坐标为($\frac{m}{2}$,$\frac{2k}{m}$),由B、C的纵坐标间的关系可得出点D为线段OC的中点,进而得出D($\frac{m}{4}$,$\frac{k}{m}$),由△ABC和△BCD等高结合三角形的面积公式即可得出$\frac{{S}_{△ABC}}{{S}_{△BCD}}$=$\frac{BD}{AB}$,代入数值即可得出结论.
解答 解:设点B的坐标为(m,$\frac{k}{m}$),则点C的坐标为($\frac{m}{2}$,$\frac{2k}{m}$),
∴点D为线段OC的中点,点D($\frac{m}{4}$,$\frac{k}{m}$),
∴BD=m-$\frac{m}{4}$=$\frac{3m}{4}$.
∵△ABC和△BCD等高,
∴$\frac{{S}_{△ABC}}{{S}_{△BCD}}$=$\frac{BD}{AB}$=$\frac{\frac{3}{4}m}{m}$=$\frac{3}{4}$.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征、等边三角形的性质以及三角形的面积,设出点B的坐标表示出点D的坐标是解题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
 如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).
如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
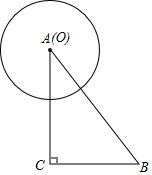 如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.
如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)-2=$-\frac{1}{4}$ | B. | $\sqrt{4}$=±2 | C. | (π-3.14)0=0 | D. | |-2|=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
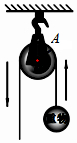 一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).
一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 众数 | 中位数 | 平均数 |
| 甲 | 6 | 6 | 6.7 |
| 乙 | 8 | 7.5 | 7.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com