
已知关于x的一元二次方程x2﹣(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得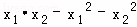 ≥0成立?若存在,请求出k的值;若不存在,请说明理由.
≥0成立?若存在,请求出k的值;若不存在,请说明理由.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
如图,有一个直角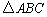 ,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线Ax上运动,当AP= 时,才能使△ABC与△PQA全等。
,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线Ax上运动,当AP= 时,才能使△ABC与△PQA全等。

查看答案和解析>>
科目:初中数学 来源: 题型:
某超市一月份的营业额为36万元,三月份的营 业额为48万元,设每月的平均增长率为x,则可列方程为( )
业额为48万元,设每月的平均增长率为x,则可列方程为( )
|
| A. | 48(1﹣x)2=36 | B. | 48(1+x)2=36 | C. | 36(1﹣x)2=48 | D. | 36(1+x)2=48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
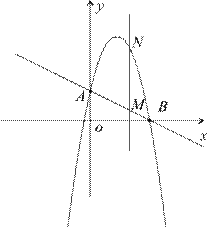
如图,一次函数 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线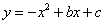 过A、B两点。(1)求这个抛物线的解析式;
过A、B两点。(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
教师节期间,某校数学组教师向本组其他教师各发一条祝福短信.据统计,全组共发了240条祝福短信,如果设全组共有x名教师,依题意,可列出的方程是( )
A.x(x+1)=240 B.x(x-1)=240 C.2x(x+1)=240 D. 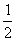 x(x-1)=240
x(x-1)=240
查看答案和解析>>
科目:初中数学 来源: 题型:
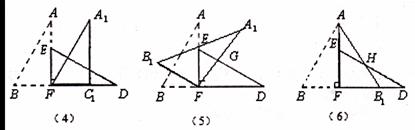
如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30。再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)
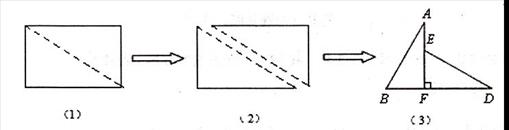
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A.F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB,交DE丁点H,请证明:AH=DH。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图3,在矩形ABCD中,动点P从B点以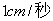 速度出发,沿BC、CD、DA运动到A点停止,设点P运动时间为
速度出发,沿BC、CD、DA运动到A点停止,设点P运动时间为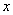 秒,
秒,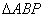 面积为
面积为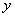
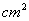 ,
,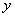 关于
关于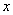 的函数图象如图4所示,则矩形ABCD面积是( )
的函数图象如图4所示,则矩形ABCD面积是( )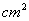
A.5 B.10 C.15 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com