
【题目】如图所示,AB是⊙O的直径,点C是![]() 中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
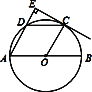
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
【答案】(1)证明见解析(2)四边形AOCD是菱形
【解析】试题分析:(1)连接OD,可证明△AOD为等边三角形,可得到∠EAO=∠COB,可证明OC∥AE,可证得结论;
(2)利用△OCD和△AOD都是等边三角形可证得结论.
试题解析:(1)连接OD,如图,∵C是![]() 的中点,∴∠BOC=∠COD=60°,∴∠AOD=60°,且OA=OD,
的中点,∴∠BOC=∠COD=60°,∴∠AOD=60°,且OA=OD,
∴△AOD为等边三角形,∴∠EAB=∠COB,∴OC∥AE,∴∠OCE+∠AEC=180°,∵CE⊥AE,∴∠OCE=180°﹣90°=90°,即OC⊥EC,∵OC为圆的半径,∴CE为圆的切线;
(2)四边形AOCD是菱形,理由如下:由(1)可知△AOD和△COD均为等边三角形,
∴AD=AO=OC=CD,∴四边形AOCD为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 | 4 | 2,3 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张试卷共有25道题,若做对1题得4分,做错1题扣1分,小明做了全部试题只得了70分,那么小明做对了( )
A. 17道 B. 18道 C. 19道 D. 20道
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 两条直线被第三条直线所截,内错角相等
B. 平行四边形的对角线相等
C. 三角形的外心到三角形三个顶点的距离相等
D. 对角线互相垂直的四边形是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com