
 已知直线y=
已知直线y=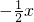 与抛物线y=
与抛物线y=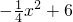 交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为
交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为
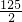
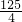
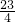
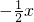 与抛物线y=
与抛物线y=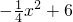 可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.
可以求出A、B两点的坐标,过点A作AM∥x轴,交抛物线于点M,作MC⊥AM于C交x轴于点E,作PD⊥AM点D,交x轴于点F,则S△ABP=S四边形BCDP+S△PDA-S△ABC,就可以求出其值.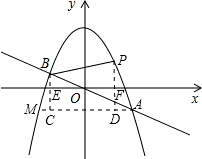 解:由题意,得
解:由题意,得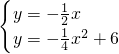
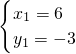 ,
,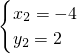 ,
, a2+6),
a2+6), a2+9,AD=6-a,
a2+9,AD=6-a,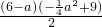 ,
,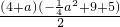
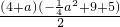 +
+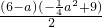 -25
-25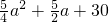

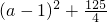 ,
,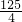 ,故C答案正确.
,故C答案正确.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
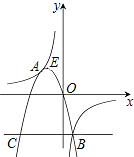 (2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线y=
(2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省温州市九年级(上)期中数学试卷(解析版) 题型:选择题
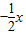 与抛物线y=
与抛物线y=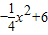 交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为( )
交于A、B两点,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中存在一个面积最大的三角形,最大面积为( )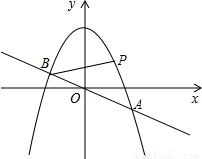
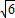
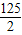
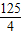
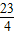
查看答案和解析>>
科目:初中数学 来源:2012年内蒙古呼和浩特市中考数学试卷(解析版) 题型:解答题
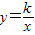 相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.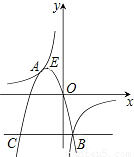
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com