
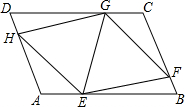
 如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.分析 (1)由全等三角形的判定定理SAS证得结论;
(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
解答 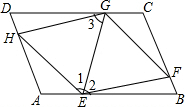 (1)证明:如图,∵四边形ABCD是平行四边形,
(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
$\left\{\begin{array}{l}{AE=CG}\\{∠A=∠C}\\{AH=CF}\end{array}\right.$,
∴△AEH≌△CGF(SAS);
(2)解:∵在ABCD中∠B=∠D,且AB=CD AD=BC
又∵AE=CG AH=CF,
∴BE=DG DH=BF,
∴△DHG≌△BFE,
∴HG=EF
又∵HE=GF
∴四边形EFGH是平行四边形
又∵EG平分∠HEF,
∴∠1=∠2
又∵HG∥EF,
∴∠2=∠3,
∴∠1=∠3,
∴HE=HG,
∴EFGH是菱形;
点评 本题考查了全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定.解题的关键是掌握两组对边相等的四边形是平行四边形,一组邻边相等的平行四边形是菱形.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
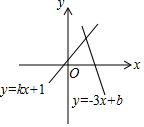 一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )
一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )| A. | 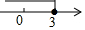 | B. | 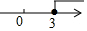 | C. | 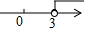 | D. | 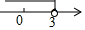 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
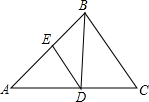 如图,△ABC中,∠A=36°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,
如图,△ABC中,∠A=36°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com