
 .求腰AB的长.
.求腰AB的长.
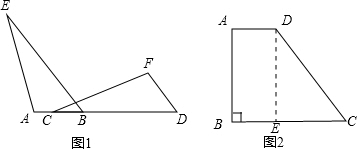
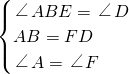 ,
, =4.
=4.

科目:初中数学 来源: 题型:
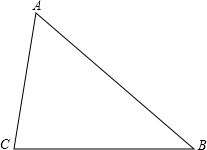 如图,在△ABC中,∠B=40°,∠C=80°,按要求完成下列各题:
如图,在△ABC中,∠B=40°,∠C=80°,按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:
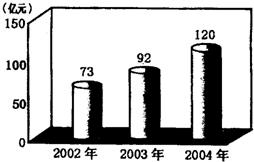 下图显示的是今年2月25日《太原日报》刊登的太原市2002年至2004年财政总收入完成情况,图中数据精确到1亿元,根据图中数据完成下列各题:
下图显示的是今年2月25日《太原日报》刊登的太原市2002年至2004年财政总收入完成情况,图中数据精确到1亿元,根据图中数据完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•泰宁县质检)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(2012•泰宁县质检)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
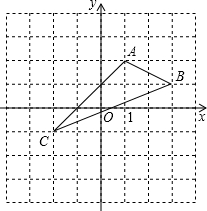 如图,在平面直角坐标系中完成下列各题:
如图,在平面直角坐标系中完成下列各题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com