
| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
分析 (1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50<x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,套入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当1≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50<x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
解答 解:(1)设每天的销售量p与时间x的函数关系式为p=mx+n
∵p=mx+n过点(60,80)、(30,140),
∴$\left\{\begin{array}{l}{60m+n=80}\\{30m+n=140}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=200}\end{array}\right.$,
∴p=-2x+200(0≤x≤90,且x为整数),
当0≤x≤50时,w=(y-30)•p=(x+40-30)(-2x+200)=-2x2+180x+2000;
当50<x≤90时,w=(90-30)(-2x+200)=-120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是w=$\left\{\begin{array}{l}{-2{x}^{2}+180X+2000}&{(0≤x≤50,且x为整数)}\\{-120x+12000}&{(50<x≤90,且x为整数)}\end{array}\right.$.
(2)当0≤x≤50时,w=-2x2+180x+2000=-2(x-45)2+6050,
∵a=-2<0且0≤x≤50,
∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,w=-120x+12000,
∵k=-120<0,w随x增大而减小,
∴当x=50时,w取最大值,最大值为6000元.∵6050>6000,
∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当0≤x≤50时,令w=-2x2+180x+2000≥5600,即-2x2+180x-3600≥0,
解得:30≤x≤50,50-30+1=21(天);
当50<x≤90时,令w=-120x+12000≥5600,即-120x+6400≥0,
解得:50<x≤53$\frac{1}{3}$,
∵x为整数,
∴50<x≤53,53-50=3(天).
综上可知:21+3=24(天),
故该商品在销售过程中,共有24天每天的销售利润不低于5600元.
点评 本题考查了二次函数的应用、一元一次不等式的应用、一元二次不等式的应用以及利用待定系数法求函数解析式,解题的关键:(1)根据点的坐标利用待定系数法求出函数关系式;(2)利用二次函数与一次函数的性质解决最值问题;(3)得出关于x的一元一次和一元二次不等式.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,根据给定数量关系,找出函数关系式是关键.


科目:初中数学 来源: 题型:解答题
 多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(-1,-2),你能帮她建立平面直角坐标系并求出其他各景点的坐标?(图中每个小正方形的边长为1 )
多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(-1,-2),你能帮她建立平面直角坐标系并求出其他各景点的坐标?(图中每个小正方形的边长为1 )查看答案和解析>>
科目:初中数学 来源: 题型:解答题
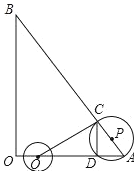 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com