阅读下列范例,按要求解答问题.
例:已知实数a、b、c满足a+b+2c=1,a
2+b
2+6c+
=0,求a、b、c的值.
解法1:由已知得a+b=1-2c,①(a+b)
2-2ab+6c+
=0.②
将①代入②,整理得4c
2+2c-2ab+
=0.∴ab=2c
2+c+
③
由①、③可知,a、b是关于t的方程t
2-(1-2c)t+2c
2+c+
=0④的两个实数根.
∴△=(1-2c)
2-4(2c
2+c+
≥0,即(c+1)
2≤0.而(c+1)
2≥0,∴c+l=0,c=-1,
将c=-1代入④,得t
2-3t+
=0.∴t
1=t
2=
,即a=b=
.∴a=b,c=-1.
解法2∵a+b+2c=1,∴a+b=1-2c、设a=
+t,b=
-t.①
∵a
2+b
2+6c+
=0,∴(a+b)
2-2ab+6c+
=0.②
将①代入②,得(1-2c)
2-2
(+t)(-t)+6c+
=0.
整理,得t
2+(c
2+2c+1)=0,即t
2+(c+1)
2=0.∴t=0,c=-1.
将t、c的值同时代入①,得a=
,b=
.a=b=
,c=-1.
以上解法1是构造一元二次方程解决问题.若两实数x、y满足x+y=m,xy=n,则x、y是关于t的一元二次方程t
2-mt+n=0的两个实数根,然后利用判别式求解.
以上解法2是采用均值换元解决问题.若实数x、y满足x+y=m,则可设x=
+t,y=
-t.一些问题根据条件,若合理运用这种换元技巧,则能使问题顺利解决.
下面给出两个问题,解答其中任意一题:
(1)用另一种方法解答范例中的问题.
(2)选用范例中的一种方法解答下列问题:
已知实数a、b、c满足a+b+c=6,a
2+b
2+c
2=12,求证:a=b=c.

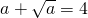 ,b2+b=4,则
,b2+b=4,则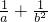 的值是
的值是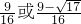
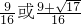
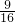
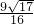
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案