
 ��ͼ��������y=ax2+bx+c������A��5��0����B��-3��0����C��0��4����
��ͼ��������y=ax2+bx+c������A��5��0����B��-3��0����C��0��4�������� ��1������������y=ax2+bx+c����A��5��0����B��-3��0�������ô���ϵ��������������ߵĺ�����ϵʽΪy=-$\frac{4}{15}$��x+3����x-5����
��2�����ȸ���C��0��4����CD��x�ύ��������D�����CD=2���ٸ��ݵ�Q��λ�÷���������������ۣ���Q��BC���˶�����Q��CD���˶������������ε�������㹫ʽ���ֱ����S��t�ĺ�����ϵʽ���ڸ��ݢ������õ�S��t�ĺ�����ϵʽ���ֱ����S�����ֵ������ۺϣ������������ɵã���t=4ʱ��S�����ֵ�����ֵΪ$\frac{32}{5}$���۷���������������ۣ���Q���߶�BC�ϣ�����C�غϣ�����Q��C�غϣ��������������ε����ʣ��ֱ����t��ֵΪ3��5��
��� ��1����������y=ax2+bx+c����A��5��0����B��-3��0����
����y=a��x+3����x-5����
��4=a��0+3����0-5����
���a=-$\frac{4}{15}$��
�������ߵĺ�����ϵʽΪy=-$\frac{4}{15}$��x+3����x-5����
��$y=-\frac{4}{15}{x^2}+\frac{8}{15}x+4$��
��2���١�C��0��4����CD��x�ύ��������D��
���D��������Ϊ4��
��y=4ʱ��4=-$\frac{4}{15}$��x+3����x-5����
���x1=0��x2=2��
��D��2��4����
��CD=2��
��������0��t��5ʱ��QB=t��PB=8-t��
��ͼ������Q��QF��x����F����QF=$\frac{4}{5}t$��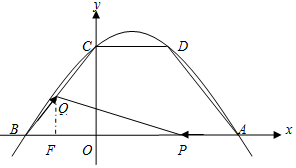
��S=$\frac{1}{2}$PB•QF=$\frac{1}{2}��8-t��•\frac{4}{5}t$=$-\frac{2}{5}{t^2}+\frac{16}{5}t$��
��������5��t��7ʱ��Q���������Ϊ4��PB=8-t��
��S=$\frac{1}{2}��8-t����4$=-2t+16��
�ڣ�������0��t��5ʱ��$S=-\frac{2}{5}{t^2}+\frac{16}{5}\;t=-\frac{2}{5}{��t-4��^2}+\frac{32}{5}$��
��-$\frac{2}{5}$��0��
�൱t=4ʱ��S�����ֵ�����ֵS=$\frac{32}{5}$��
��������5��t��7ʱ��S=-2t+16��
��-2��0��
��S����t�����������
�൱t=5ʱ��S�����ֵ�����ֵs=6��
�ۺϣ������������ɵã���t=4ʱ��S�����ֵ�����ֵΪ$\frac{32}{5}$��
�۴���������tֵ��ʹ�á�PQB��ֱ�������Σ�
����Q���߶�BC�ϣ�����C�غϣ�ʱ��Ҫʹ�á�PQB��ֱ�������Σ�����ʹ�á�PQB=90�㣬
��ʱ��BOC����BQP��
��$\frac{BQ}{BP}=\frac{OB}{BC}$��
��$\frac{t}{8-t}=\frac{3}{5}$��
��t=3��
����Q��C�غ�ʱ����P���OҲ�غϣ�
����PBQ���OBC�غϣ�����Ҫ��
��ʱt=5��1=5��
����������t��ֵΪ3��5��
���� �������ڶ��κ����ۺ��⣬��Ҫ�����˴���ϵ�����������߽���ʽ�����������ε��������ж������κ���ͼ�������ʵ��ۺ�Ӧ�ã��������Ĺؼ����������߹���ֱ�������Σ����������ε�������㹫ʽ������⣮����ʱע���������˼������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{AO}$ | B�� | $\overrightarrow{DO}$ | C�� | $\overrightarrow{CO}$ | D�� | $\overrightarrow{BO}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
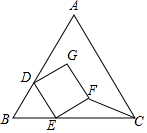 ��ͼΪ�ȱߡ�ABC��������DEFG���ص����Σ�����D��E����ֱ���AB��BC�ϣ���BD=BE����AB=3��DE=1�����EFC�����Ϊ��������
��ͼΪ�ȱߡ�ABC��������DEFG���ص����Σ�����D��E����ֱ���AB��BC�ϣ���BD=BE����AB=3��DE=1�����EFC�����Ϊ��������| A�� | $\frac{1}{4}$ | B�� | 1 | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com