
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
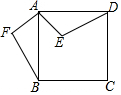 如图,点E是正方形ABCD内的一点,将△ADE绕点A顺时针旋转90°至△ABF.
如图,点E是正方形ABCD内的一点,将△ADE绕点A顺时针旋转90°至△ABF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
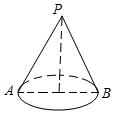 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).
如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是65πcm2(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com