
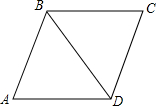
 如图,在菱形ABCD中,∠BAC=30°,则∠B=120度.
如图,在菱形ABCD中,∠BAC=30°,则∠B=120度.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
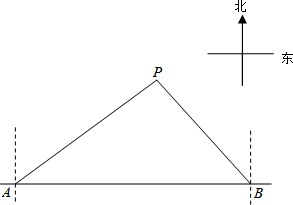 马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60.8×104 | B. | 6.08×104 | C. | 0.608×106 | D. | 6.08×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com