
 的图象过点
的图象过点 .
.
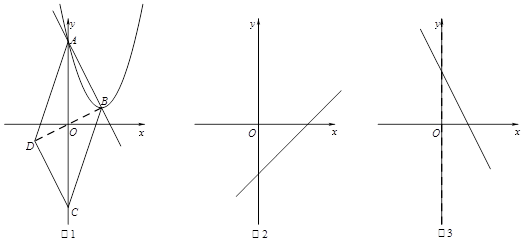
 是直角三角形;
是直角三角形;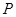 在第二象限,且是抛物线上的一动点,过点
在第二象限,且是抛物线上的一动点,过点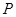 作
作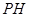 垂直
垂直 轴于点
轴于点 ,试探究是否存在以
,试探究是否存在以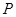 、
、 、
、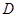 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出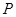 点的坐标.若不存在,请说明理由.
点的坐标.若不存在,请说明理由.
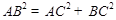 ,即有△ACB是直角三角形
,即有△ACB是直角三角形 ),(
),(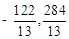 )
)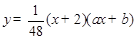 的图象
的图象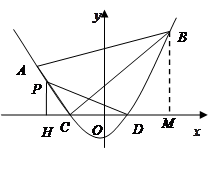
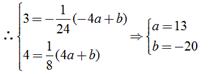

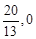 ),
), 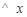 轴于点M, ∴
轴于点M, ∴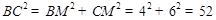 ,
, 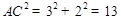 ,
, 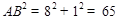 ,
,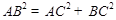 ,即有△ACB是直角三角形.
,即有△ACB是直角三角形. 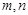 ),易得
),易得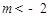 ,则
,则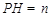 ,
,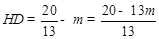
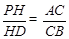 时,
时, 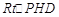 ∽
∽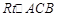 ,
,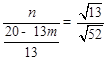 , ∴
, ∴ .
.  ,∴
,∴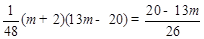 .
.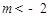 ,
,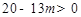 ,∴
,∴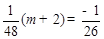 ,
,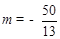 ,则
,则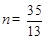 ,P点的坐标为(
,P点的坐标为( )
) 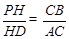 时,
时, 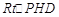 ∽
∽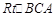 ,
,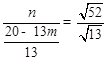 ,∴
,∴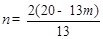 .
. ,∴
,∴ .
.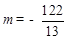 ,则
,则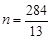 ,P点的坐标为(
,P点的坐标为(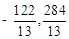 )
) ),(
),(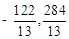 ).
). 

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (吨)与月份
(吨)与月份 (
( ,且
,且 取整数)之间满足的函数关系如下表:
取整数)之间满足的函数关系如下表:月份 (月) (月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量 (吨) (吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
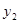 (吨)与月份
(吨)与月份 (
(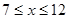 ,且
,且 取整数)之间满足二次函数关系式
取整数)之间满足二次函数关系式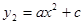 ,其图象如图所示.1至6月,污水厂处理每吨污水的费用
,其图象如图所示.1至6月,污水厂处理每吨污水的费用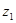 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式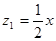 ,该企业自身处理每吨污水的费用
,该企业自身处理每吨污水的费用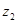 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式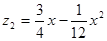 ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.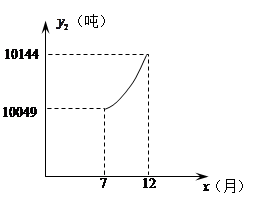
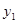 ,
,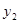 与
与 之间的函数关系式;
之间的函数关系式; 月用于污水处理的费用为W(元),试求出W与
月用于污水处理的费用为W(元),试求出W与 之间的函数关系式;
之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过点A(-1,0),B(3,0),交
经过点A(-1,0),B(3,0),交 轴于点C,M为抛物线的顶点,连接MB.
轴于点C,M为抛物线的顶点,连接MB.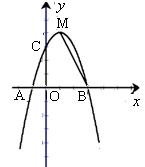
 轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由;
轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由; ,求
,求 的度数.
的度数.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= . 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
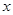 轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )

A.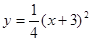 |
B. |
C.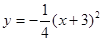 |
D.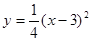 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com