
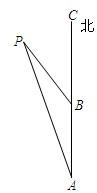
 23、如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
23、如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由. 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
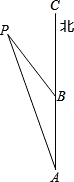 如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.查看答案和解析>>
科目:初中数学 来源: 题型:
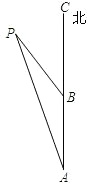
 如图:一艘轮船在上午8时从A处出发,以20海里/时的速度由南向北航行,在A处测得小岛P在北偏西24°,9点30分到达B处,这时测得小岛P在北偏西48°,求B处到小岛P的距离.
如图:一艘轮船在上午8时从A处出发,以20海里/时的速度由南向北航行,在A处测得小岛P在北偏西24°,9点30分到达B处,这时测得小岛P在北偏西48°,求B处到小岛P的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
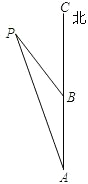
 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com