

分析 (1)根据△PEN为等腰三角形,分PE=PN,PE=EN,PN=EN三种情况求出∠DEM所有可能的值即可;
(2)如图1,过E作EF⊥BC于F,连接MN,利用同角的余角相等得到一对角相等,再由一对直角相等,且夹边相等,利用ASA得到三角形PEF与三角形MED全等,利用全等三角形对应边相等得到PE=DM=1,EP=EM,再利用SAS得到三角形EPN与三角形EMN全等,利用全等三角形对应边相等得到MN=PN,即可求出PN的长;
(3)如图2,易知DK=$\frac{1}{2}$EM,PG=$\frac{EP}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$EM,连接GM,利用SAS得到三角形EPG与三角形PEG全等,利用全等三角形对应角相等,表示出GK,分别代入原式变形后,根据EM的范围求出最大值与最小值即可.
解答 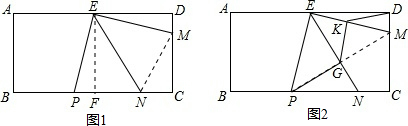 解:(1)若△PEN为等腰三角形,∠DEM所有可能的值为0°,22.5°,45°;
解:(1)若△PEN为等腰三角形,∠DEM所有可能的值为0°,22.5°,45°;
(2)如图1,过E作EF⊥BC于F,连接MN,
∵EF⊥AD,PE⊥EM,
∴∠PEF+∠FEM=90°,∠FEM+∠DEM=90°,
∴∠PEF=∠MED,
∵AD=2AB,E为AD中点,且EF=AB,
∴EF=ED,
在△PEF和△MED中,
$\left\{\begin{array}{l}{∠PEF=∠MED}\\{EF=ED}\\{∠EFP=∠D=90°}\end{array}\right.$,
∴△EPF≌△EMD(ASA),
∴PF=DM=1,EP=EM,
在△EPN和△EMN中,
$\left\{\begin{array}{l}{EP=EM}\\{∠PEN=∠MEN}\\{EN=EN}\end{array}\right.$,
∴△EPN≌△EMN(SAS),
∴MN=PN,
在△CMN中,由勾股定理有CN2+CM2=MN2,即(7-PN)2+52=PN2,
解得:PN=$\frac{37}{7}$;
(3)如图2,易知DK=$\frac{1}{2}$EM,PG=$\frac{EP}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$EM,
连接GM,
在△EMG和△EPG中,
$\left\{\begin{array}{l}{EP=EM}\\{∠PEG=∠MEG}\\{EG=EG}\end{array}\right.$,
∴△EMG≌△EPG(SAS),
∴∠EGM=∠EGP=90°,
∴GK=$\frac{1}{2}$EM,
∴DK+KG+GP=$\frac{1}{2}$EM+$\frac{1}{2}$EM+$\frac{\sqrt{2}}{2}$EM=(1+$\frac{\sqrt{2}}{2}$)EM(6≤EM≤6$\sqrt{2}$),
则DK+KG+GP的最大值为6+6$\sqrt{2}$,最小值为6+3$\sqrt{2}$.
点评 此题属于四边形综合题,涉及的知识有:矩形的性质,勾股定理,全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,BC=2AD,过点A作AE∥DC交BC于点E.
如图,在梯形ABCD中,AD∥BC,BC=2AD,过点A作AE∥DC交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O中,AB是直径,PA和PC分别与⊙O相切于A,C两点,连结OP,CB
如图,已知⊙O中,AB是直径,PA和PC分别与⊙O相切于A,C两点,连结OP,CB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).
如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种客车 | 乙种客车 | |
| 载客量/(人/辆) | 45 | 30 |
| 租金/(元/辆) | 400 | 280 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com