
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
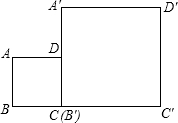
 18、如图,现有两个边长之比为1:2的正方形ABCD与A′B′C′D′,点B、C、B′、C′在同一直线上,且点C与点B′重合,能否利用这两个正方形,通过裁割、平移、旋转的方法,拼出两个相似比为1:3的三角形?
18、如图,现有两个边长之比为1:2的正方形ABCD与A′B′C′D′,点B、C、B′、C′在同一直线上,且点C与点B′重合,能否利用这两个正方形,通过裁割、平移、旋转的方法,拼出两个相似比为1:3的三角形?查看答案和解析>>
科目:初中数学 来源: 题型:044
现有一张边长之比为1:2的矩形纸片,将它折两次(第一次折后,也可打开铺平再折第二次),使得折痕将纸片分成拿等的四个部分(称为一个操作),如图(1)(虚线表示折痕).除图(1)外,请你再给出三个不同的操作,分别将折痕画在图(3)的①~③中,(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图(2)和图(1)是相同的操作)

查看答案和解析>>
科目:初中数学 来源:2010年河北省保定市中考数学三模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年天津市河北区中考数学一模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com