
分析 先把解析式配成顶点式得到抛物线的顶点坐标为(-$\frac{1}{2}$m,-$\frac{1}{4}$m2+n),再根据题意得到-$\frac{1}{2}$m=-$\frac{1}{4}$m2+n,($\frac{1}{2}$m)2+(-$\frac{1}{4}$m2+n)2=8,然后解关于m的一元二次方程即可.
解答 解:∵y=x2+mx+n=(x+$\frac{1}{2}$m)2-$\frac{1}{4}$m2+n,
∴抛物线的顶点坐标为(-$\frac{1}{2}$m,-$\frac{1}{4}$m2+n),
∵二次函数y=x2+mx+n的图象的顶点在第一象限内的直线y=x上,且到原点的距离为2$\sqrt{2}$,
∴-$\frac{1}{2}$m=-$\frac{1}{4}$m2+n,($\frac{1}{2}$m)2+(-$\frac{1}{4}$m2+n)2=8,
∴m=±4(正值舍去),即m=-4,
∴此二次函数的解析式为y=(x-2)2+2,即y=x2-4x+6.
故答案为y=x2-4x+6.
点评 本题考查的是用待定系数法求二次函数的解析式以及二次函数的性质,难度适中.利用配方法得到抛物线的顶点坐标为(-$\frac{1}{2}$m,-$\frac{1}{4}$m2+n)是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
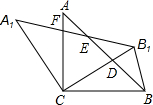 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设B1C交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设B1C交AB于D,A1B1分别交AB,AC于E,F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时刻 | 9:00 | 9:48 | 11:00 |
| 里程碑上的数 | 是一个两位数,它的两个数字之和为6 | 也是一个两位数,十位与个位数字与9:00时所看到的正好互换了 | 是一个三位数,比9:00时看到的两位数的数字中间多了个0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
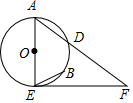 如图,AE为⊙O的直径,D为$\widehat{AB}$的中点,过E点的切线交AD的延长线于F.
如图,AE为⊙O的直径,D为$\widehat{AB}$的中点,过E点的切线交AD的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
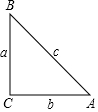 如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.
如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com