
如果反比例函数 的图象如图所示,那么二次函数y=kx2-k2x-1的图象大致为( )
的图象如图所示,那么二次函数y=kx2-k2x-1的图象大致为( )
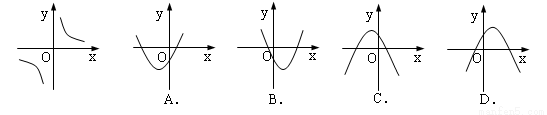
B.
【解析】
试题分析:根据反比例函数图象可知k>0,
由y=kx2-k2x-1,配方得y=k(x-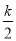 )2-1,
)2-1,
开口向上,且对称轴x=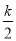 >0,在y轴右侧.
>0,在y轴右侧.
故选B.
考点:1.二次函数的图象;2.反比例函数的图象.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源:2014-2015学年福建省八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,羊字象征吉祥和美满,下图的图案与羊有关,其中是轴对称的有( )
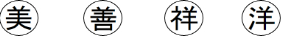
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省八年级下学期开学考试数学试卷(解析版) 题型:选择题
直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )
A.2个 B.1个 C.4个 D.3个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
三角形两边长分别为3和6,第三边是方程x2﹣6x+8=0的解,则这个三角形的周长_____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:① PA=PB+PC,② 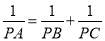 ;③ PA·PE=PB·PC.其中,正确结论的个数为( )。
;③ PA·PE=PB·PC.其中,正确结论的个数为( )。
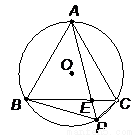
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分10分)
猜想与证明:
如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
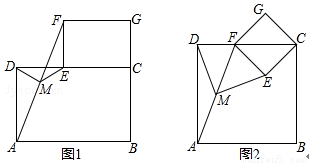
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
下列运算正确的是( ).
A.a3+a4=a7 B.2a3a4=2a7 C.(2a4)3=8a7 D.a8÷a2=a4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:选择题
观察上面的图形,它们是按一定规律排列的,依照此规律,第( )个图形共有120 个.

A.10 B.13 C.15 D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com