
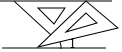
 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )| A. | 30° | B. | 20° | C. | 15° | D. | 14° |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
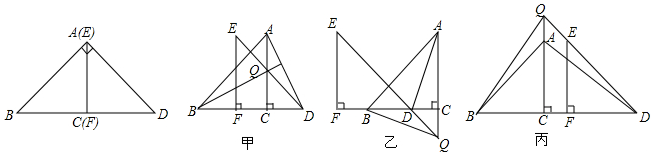
 如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
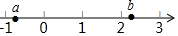 已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )
已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )| A. | -2a | B. | -2b | C. | -2a-b | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
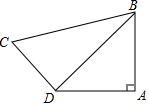 如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
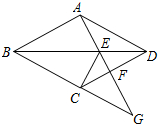 如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
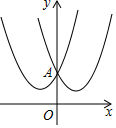 如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.
如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com