
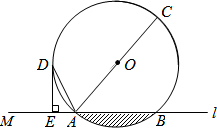
 如图,直线l与⊙O相交于A,B两点,AC是⊙O的直径,D是⊙O上一点,DE⊥l于点 E,连结AD,且AD平分∠CAM.
如图,直线l与⊙O相交于A,B两点,AC是⊙O的直径,D是⊙O上一点,DE⊥l于点 E,连结AD,且AD平分∠CAM. ,求⊙O的半径;
,求⊙O的半径;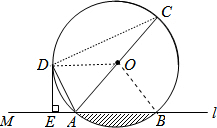
 ,
,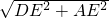 =
= =4
=4 ,
, =
= ,即
,即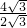 =
=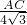 ,
, .
. ;
; ,AD=4
,AD=4 ,
,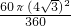 -
- ×(4
×(4 )2
)2 .
. .
. ,由AC是⊙O直径得到∠ADC=90°,易证得△ACD∽△ADE,利用相似比可计算出AC,即可得到圆的半径;
,由AC是⊙O直径得到∠ADC=90°,易证得△ACD∽△ADE,利用相似比可计算出AC,即可得到圆的半径; ,AD=4
,AD=4 可得∠AED=60°,而AD平分∠CAM,易得∠EAO=120°,则∠OAB=60°,所以△OAB为等边三角形,于是∠AOB=60°,
可得∠AED=60°,而AD平分∠CAM,易得∠EAO=120°,则∠OAB=60°,所以△OAB为等边三角形,于是∠AOB=60°,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2013•相城区模拟)如图,直线l与圆O相交于A,B两点,与y轴交于点P.若点A的坐标为(1,3),PB=3PA,则直线l的解析式为
(2013•相城区模拟)如图,直线l与圆O相交于A,B两点,与y轴交于点P.若点A的坐标为(1,3),PB=3PA,则直线l的解析式为查看答案和解析>>
科目:初中数学 来源:2011-2012学年陕西宝鸡金台区七年级下学期期中数学试卷(解析版) 题型:选择题
如图,直线AB与CD相交于点O,EO⊥CD,垂足为O,则图中∠AOE和∠BOD的关系是( )

A.相等角 B.互为补角 C.对顶角 D.互为余角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com