Question

3．图1、图2分别由两个长方形拼成．

（1）图1中图形的面积为a²-b²，图2中图形的面积为（a-b）×（a+b）；（用含有a、b的代数式表示）
（2）由（1）可以得到等式：a²-b²=（a+b）（a-b）；
（3）根据你得到的等式解决下列问题：
 ①计算：68.5²-31.5² ②若m+4n=2，求（m+1）²+（2n+1）²-m²-（2n-1）²的值．

Answer 1

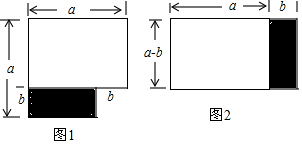
分析 （1）图2面积根据长方形面积公式可得；
（2）根据两个图形的面积相等可得；
（3）①直接套用公式a²-b²=（a-b）（a+b）可得；②将原式变形为[（m+1）²-m²]+[2n+1）²（2n-1）²]，再套用平方差公式可得答案．

解答 解：（1）图1中图形的面积为a²-b²，图2中图形的面积为（a-b）×（a+b），
故答案为：a+b；

（2）根据两个图形的面积相等可得a²-b²=（a-b）（a+b），
故答案为：a²-b²=（a-b）（a+b）；

（3）①68.5²-31.5²=（68.5-31.5）（68.5+31.5）=35×100=3500；
②（m+1）²+（2n+1）²-m²-（2n-1）²=[（m+1）²-m²]+[2n+1）²（2n-1）²]
=[（m+1-m）（m+1+m）]+[（2n+1-2n+1）（2n+1+2n-1）]
=2m+1+8n
=4+1
=5．

点评 本题主要考查平方差公式的几何背景，运用几何直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．