
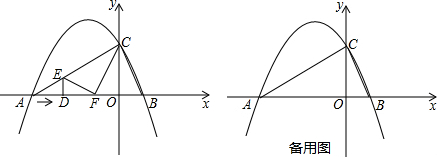
分析 (1)把A(-4,0),B(1,0),点C(0,2)即可得到结论;
(2)由题意得AD=2t,DF=AD=2t,OF=4-4t,由于直线AC的解析式为:y=$\frac{1}{2}$x+2,得到E(2t-4,t),①当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质得到结论;②当∠FEC=90°,根据等腰直角三角形的性质得到结论;③当∠ACF=90°,根据勾股定理得到结论;
(3)求得直线BC的解析式为:y=-2x+2,当D在y轴的左侧时,当D在y轴的右侧时,如图2,根据梯形的面积公式即可得到结论.
解答 解:(1)把A(-4,0),B(1,0),点C(0,2)代入y=ax2+bx+c得,$\left\{\begin{array}{l}{16a-4b+c=0}\\{a+b+c=0}\\{c=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2-$\frac{3}{2}$bx+2,
对称轴为:直线x=-$\frac{3}{2}$;
(2)存在,
∵AD=2t,
∴DF=AD=2t,
∴OF=4-4t,
∴D(2t-4,0),
∵直线AC的解析式为:y=$\frac{1}{2}$x+2,
∴E(2t-4,t),
∵△EFC为直角三角形,
①当∠EFC=90°,则△DEF∽△OFC,
∴$\frac{DE}{OF}=\frac{DF}{OC}$,即$\frac{t}{4-4t}$=$\frac{2t}{2}$,
解得:t=$\frac{3}{4}$,
②当∠FEC=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴DE=$\frac{1}{2}$AF,即t=2t,
∴t=0,(舍去),
③当∠ACF=90°,
则AC2+CF2=AF2,即(42+22)+[22+(4t-4)2]=(4t)2,
解得:t=$\frac{5}{4}$,
∴存在某一时刻t,使得△EFC为直角三角形,此时,t=$\frac{3}{4}$或$\frac{5}{4}$;
(3)∵B(1,0),C(0,2),
∴直线BC的解析式为:y=-2x+2,
当D在y轴的左侧时,S=$\frac{1}{2}$(DE+OC)•OD=$\frac{1}{2}$(t+2)•(4-2t)=-t2+4 (0<t<2),
当D在y轴的右侧时,如图2,
∵OD=4t-4,DE=-8t+10,
S=$\frac{1}{2}$(DE+OC)•OD=$\frac{1}{2}$(-8t+10+2)•(4t-4)=-16t2+40t-24 (2<t<$\frac{5}{2}$).
点评 本题考查了待定系数法确定函数关系式,梯形的面积公式,直角三角形的性质,相似三角形的判定和性质,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
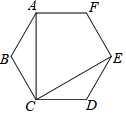
 如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=2CD,点E,F分别为AB,AD的中点,则三角形AEF与多边形BCDFE的面积之比为( )
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=2CD,点E,F分别为AB,AD的中点,则三角形AEF与多边形BCDFE的面积之比为( )| A. | 1:7 | B. | 1:6 | C. | 1:5 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | -$\sqrt{2}$+1 | C. | -$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
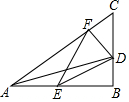 如图,△ABC中,∠B=90°,∠C=60°,AD平分∠BAC交BC于D,过D作DF⊥AC于F,E在AB上,且DE=AE,连结EF.若AB=4+2$\sqrt{3}$,则EF的长为( )
如图,△ABC中,∠B=90°,∠C=60°,AD平分∠BAC交BC于D,过D作DF⊥AC于F,E在AB上,且DE=AE,连结EF.若AB=4+2$\sqrt{3}$,则EF的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.
2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com