
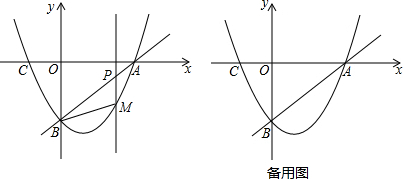
���� ��1�����A��B�������꣬��������ʽ�������ߵĽ���ʽΪy=a��x+1����x-3������B��0��-3�����뼴�ɽ�����⣮
��2������ͼ1�У���P��t��t-3����M��t��t2-2t-3��������s=S��PMB+S��PMA���㼴�ɣ�
�������䷽�������ݶ��κ��������ʼ��ɽ�����⣮
����ͼ2�У���BH��PM��H����ΪBP=BM��BH��PM���Ƴ�PH=KM����P��t��t-3����M��t��t2-2t-3�������ݵ�H��������Ϊ-3���ɵ÷��̣�$\frac{t-3+{t}^{2}-2t-3}{2}$=-3���ⷽ�̼��ɽ�����⣮
��� �⣺��1����ֱ��y=x-3��x���y��ֱ���A��B���㣬
��A��3��0����B��0��-3����
����������x�ύ�ڵ�A��3��0����C��-1��0����
����Լ��������ߵĽ���ʽΪy=a��x+1����x-3������B��0��-3������ã�-3=-3a��
��a=1��
�������ߵĽ���ʽΪy=x2-2x-3��
��2������ͼ1�У���P��t��t-3����M��t��t2-2t-3����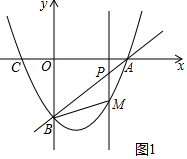
��PM=t-3-��t2-2t-3��=-t2+3t��
��s=S��PMB+S��PMA=$\frac{1}{2}$•��-t2+3t��•3=-$\frac{3}{2}$t2+$\frac{9}{2}$t��0��t��3����
�ڴ��ڣ��������£���s=-$\frac{3}{2}$t2+$\frac{9}{2}$t=-$\frac{3}{2}$��t-$\frac{3}{2}$��2+$\frac{27}{8}$��
��-$\frac{3}{2}$��0��
��t=$\frac{3}{2}$ʱ��s�����ֵ�����ֵ=$\frac{27}{8}$��
����ͼ2�У���BH��PM��H��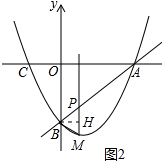
��BP=BM��BH��PM��
��PH=KM��
��P��t��t-3����M��t��t2-2t-3����
���H��������Ϊ$\frac{t-3+{t}^{2}-2t-3}{2}$=-3��
���t=1��0����������
��t=1ʱ����PBM���Ե�BΪ����ĵ��������Σ���ʱP��1��-2����
���� ���⿼����κ����ۺ��⡢����ϵ�����������ε���������������ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ�����ӳ��ø����ߣ�ѧ�������ת��Ϊ���̽���������п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AB=4����O���߶�AB�ϵĵ㣬��C��D���߶�OA��OB���е㣬С�������ɵ����CD=2�����ڷ�˼������ͻ�����룺����O��AB�ӳ������˶�ʱ��ԭ�еĽ��ۡ�CD=2������Ȼ�����أ����С������ͼ�η�����˵�����ɣ�
��ͼ���߶�AB=4����O���߶�AB�ϵĵ㣬��C��D���߶�OA��OB���е㣬С�������ɵ����CD=2�����ڷ�˼������ͻ�����룺����O��AB�ӳ������˶�ʱ��ԭ�еĽ��ۡ�CD=2������Ȼ�����أ����С������ͼ�η�����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
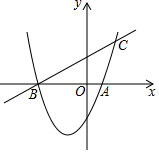 ��ͼ����֪������y=ax2+bx-2��a��0����x�ύ��A��B���㣬ֱ��BC���������ڵ�C������C������Ϊ��2��3����tan��CBA=$\frac{1}{2}$����������ߵĶԳ���Ϊֱ��x=-$\frac{3}{2}$��
��ͼ����֪������y=ax2+bx-2��a��0����x�ύ��A��B���㣬ֱ��BC���������ڵ�C������C������Ϊ��2��3����tan��CBA=$\frac{1}{2}$����������ߵĶԳ���Ϊֱ��x=-$\frac{3}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
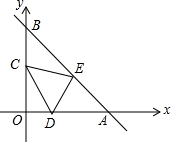 ��֪����ͼ��ֱ��y=-x+12�ֱ�x�ᡢy����A��B�㣬����AOB�۵���ʹA��ǡ������OB���е�C�����ۺ�ΪDE��
��֪����ͼ��ֱ��y=-x+12�ֱ�x�ᡢy����A��B�㣬����AOB�۵���ʹA��ǡ������OB���е�C�����ۺ�ΪDE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | 4 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com