练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
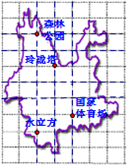
    13．我市为了促进全民健身，举办“健步走”活动，朝阳区活动场地位于奥林匹克公园（路线：森林公园-玲珑塔-国家体育场-水立方）．如图，体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为（-1，0），森林公园的坐标为（-2，2），则终点水立方的坐标为（　　）
    A．（-2，-4）B．（-1，-4）C．（-2，4）D．（-4，-1）

    分析 根据玲珑塔的坐标向右平移1个单位，可得原点坐标，根据点的位置，可得相应点的坐标．

    解答 解：如图：
    ，
    水立方的坐标为（-2，-4）．
    故选：A．

    点评 本题考查了坐标确定位置，玲珑塔的坐标向右平移1个单位得出原点坐标是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

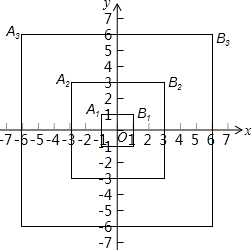    3．如图，第一个正方形的顶点A1（-1，1），B1（1，1）；第二个正方形的顶点A2（-3，3），B2（3，3）；第三个正方形的顶点A3（-6，6），B3（6，6），按顺序取点A1，B2，A3，B4，A5，B6…，则第10个点应取点B10，其坐标为（55，55），第2n-1（n为正整数）个点应取点A2n-1，其坐标为（-n（2n-1），n（2n-1））．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长（　　）
    A．7B．8C．9D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知Rt△ABC中，∠BAC=90°，M为AC的中点，N为BM中点，AN延长线交BC于P，过P作PQ∥AB交BM于Q．求证：
    （1）△AQM∽△CPA；
    （2）AQ=$\frac{1}{2}$PC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

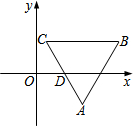    8．如图，在平面直角坐标系中，△ABC是等边三角形，BC∥x轴，AB=4，AC的中点D在x轴上，且D（$\sqrt{3}$，0），则点A的坐标为（　　）
    A．（2$\sqrt{3}$，-$\sqrt{3}$）B．（$\sqrt{3}$-1，$\sqrt{3}$）C．（$\sqrt{3}$+1，-$\sqrt{3}$）D．（$\sqrt{3}$-1，-$\sqrt{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．实数a，b在数轴上的对应点的位置如图所示，化简|a-b|的结果是（　　）
    A．0B．a+bC．a-bD．b-a

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，AB是⊙O的直径，且AB垂直弦CD于点E，点G是AB上一点，点P为AB延长线上一点，AB=8，CD=4$\sqrt{2}$．
    （1）连接GC，GD，试问当GE为何值时，△GDC是等边三角形？
    （2）填空：
    ①当GE=4-2$\sqrt{2}$，四边形GCBD是菱形；
    ②当PB=4$\sqrt{2}$-4，四边形PCOD是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．2015年我区参加中考的人数大约有8680人，将8680用科学记数法表示为8.68×103．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

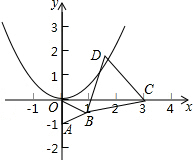    3．如图，取点A（0，-1）作等边三角形AOB（点B在第四象限），点C是x轴上一动点，作等边三角形BCD，当点D恰好落在抛物线y=$\frac{1}{2}$x2上时，点D的坐标为（$\sqrt{3}$+1，2+$\sqrt{3}$），（$\sqrt{3}-1$，2-$\sqrt{3}$）．

    查看答案和解析>>

    同步练习册答案