
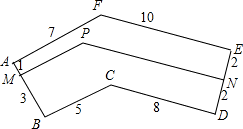
 如图:在凹六边形ABCDEF中,∠A、∠B、∠D、∠E均为直角,p是凹六边形ABCDEF内一点,PM、PN分别垂直于AB、DE,垂足分别为M、N,图中每条线段的长度如图所示(单位是米),求折线MPN的长度(精确到0.01米).
如图:在凹六边形ABCDEF中,∠A、∠B、∠D、∠E均为直角,p是凹六边形ABCDEF内一点,PM、PN分别垂直于AB、DE,垂足分别为M、N,图中每条线段的长度如图所示(单位是米),求折线MPN的长度(精确到0.01米).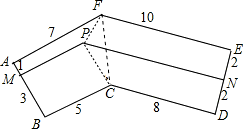 解:连接FP,PC,FC,
解:连接FP,PC,FC, •(7+x)•1+
•(7+x)•1+ •(x+5)•3+
•(x+5)•3+ •(y+8)•2+
•(y+8)•2+ (10+y)•2=
(10+y)•2= ×(7+5)×4+
×(7+5)×4+ ×(10+8)×4,
×(10+8)×4,

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com