
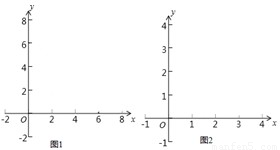
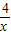 联立方程组可知,有解,所以这样的交点存在,即满足要求的矩形B存在.
联立方程组可知,有解,所以这样的交点存在,即满足要求的矩形B存在. ,xy=1,而满足要求的(x,y)可以看作一次函数y=-x+
,xy=1,而满足要求的(x,y)可以看作一次函数y=-x+ 的图象与反比例函数y=
的图象与反比例函数y=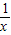 的图象在第一象限内交点的坐标.画图或联立方程组可知,这样的交点不存在,即满足要求的矩形C是不存在的.
的图象在第一象限内交点的坐标.画图或联立方程组可知,这样的交点不存在,即满足要求的矩形C是不存在的. 解:(1)点(x,y)可以看作一次函数y=-x+6的图象在第一象限内点的坐标,
解:(1)点(x,y)可以看作一次函数y=-x+6的图象在第一象限内点的坐标,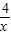 的图象在第一象限内点的坐标,
的图象在第一象限内点的坐标,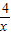 的图象在第一象限内交点的坐标.
的图象在第一象限内交点的坐标. ,xy=1,
,xy=1, 而满足要求的(x,y)可以看作一次函数y=-x+
而满足要求的(x,y)可以看作一次函数y=-x+ 的图象与反比例函数y=
的图象与反比例函数y=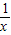 的图象在第一象限内交点的坐标.
的图象在第一象限内交点的坐标.

科目:初中数学 来源:2007年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
 时,试求出m的取值范围;
时,试求出m的取值范围; 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)
查看答案和解析>>
科目:初中数学 来源:2009年山东省日照市中考数学模拟试卷1(丁文斌)(解析版) 题型:解答题
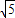 时,试求出m的取值范围;
时,试求出m的取值范围; 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)
查看答案和解析>>
科目:初中数学 来源:2007年山东省济宁市中考数学试卷(解析版) 题型:解答题
 时,试求出m的取值范围;
时,试求出m的取值范围;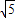 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《概率》(04)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com