
分析 (1)设制作每个乙种用x米材料,则制作甲种用(1+20%)x米材料,根据“同样用6m材料制成甲的个数比制成乙的个数少2个”,列出方程,即可解答;
(2)根据所需要材料的总长度l=甲的材料的总长度+乙的材料的总长度,列出函数关系式;再根据“甲的数量不少于乙数量的2倍”求出n的取值范围,根据一次函数的性质,即可解答.
解答 解:(1)设制作每个乙种用x米材料,则制作甲种用(1+20%)x米材料,
$\frac{6}{x}$-2=$\frac{6}{(1+20%)x}$,
解得:x=0.5,
经检验x=0.5是原方程的解,
∴(1+20%)x=0.6(米),
答:制作每个甲种用0.6米材料;制作每个乙种用0.5米材料.
(2)根据题意得:l=0.6n+0.5(3000-n)=0.1n+1500,
∵甲种的数量不少于乙种数量的2倍,
∴n≥2(3000-n)
解得:n≥2000,
∴2000≤n<3000,
∵k=0.1>0,
∴l随n增大而增大,
∴当n=2000时,l最小1700米.
点评 本题考查了一次函数的应用、分式方程的应用、不等式的应用等知识,灵活运用所学知识解决问题,注意分式方程必须检验.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
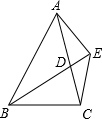 如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.
如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
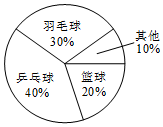 某校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢篮球的人数比最喜欢乒乓球的人数少8人,则该校被调查的学生总人数为40名.
某校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢篮球的人数比最喜欢乒乓球的人数少8人,则该校被调查的学生总人数为40名.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com