
分析 (1)设每件羽绒服的标价为x元,则10月份售出$\frac{28000}{x}$件,等量关系:11月份的销售量是10月份的1.5倍;
(2)设这批羽绒服购进a件,不等量关系:羽绒服总获利不少于9940元.
解答 解:(1)设每件羽绒服的标价为x元,则10月份售出$\frac{28000}{x}$件,
根据题意得:$\frac{28000+11000}{x-100}$=$\frac{28000}{x}$×1.5,
解得:x=1400,
经检验x=1400是原方程的解,
答:每件羽绒服的标价为1400元.
(2)设这批羽绒服购进a件,
10月份售出28000÷1400=20(件),11月份售出20×1.5=3(件)
根据题意得:28000+(11000+28000)+1400×0.9(a-20-30)-1200a≥9940
解得:a≥99,
所以a至少是99,
答:这批羽绒服至少购进99件.
点评 本题考查了分式方程的应用和一元一次不等式的应用.分析题意,找到合适的数量关系是解决问题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:选择题
| A. | (-3,2) | B. | (-2,-3) | C. | (-2,3) | D. | ( 3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 2016年铁路部门车票预售期提前到了60天并实行退改签新政.根据梯次退票政策,下表是铁路部门的退票手续费的价目表. | |
| 开车前15天(不含)以上退票的 | 不收取退票费 |
| 开车前48小时至15天以内退票的 | 收取票价5%的退票费 |
| 开车前24小时至48小时以内退票的 | 收取10%退票费 |
| 开车前24小时以内退票的 | 收取20%退票费 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
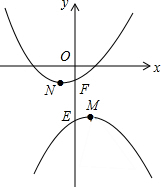 如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com